Torch DQN 강화학습 소개
작년 알파고와 이세돌간의 세기의 바둑대결이 열리면서 딥러닝(Deep Learning)이 화두가 되었고, 특히 딥마인드(DeepMind)가 강화학습(Reinforcement Learning)을 통해 알파고를 만들었다는 사실에, 강화학습이 주목을 받기 시작했다. 그리고 나도 최근에 강화 학습을 둘러보기 시작했고, 피상적으로나마 이해한 내용을 정리하고자 이 글을 썼다.
이 글에서는 강화학습과 강화학습의 알고리즘 중 하나인 DQN(Deep Q-Network)에 대해 간략히 설명한다. 그리고 딥러닝 프레임워크 중 하나인 Torch를 사용하여 스스로 "바구니로 과일 받기" 게임을 배우는 인공지능을 만드는 방법을 소개한다.
강화학습(Reinforcement Learning)
강화학습은 머신러닝 방법 중 하나다.
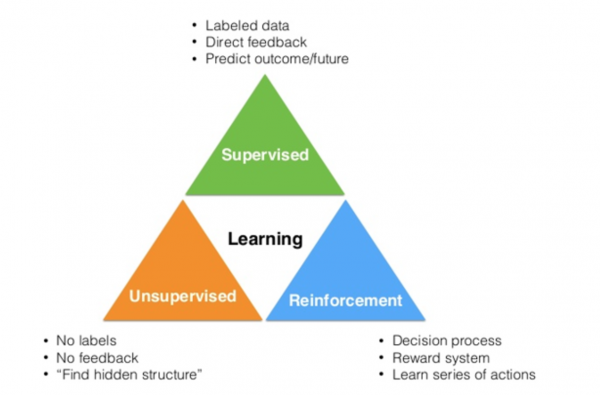
그림. 머신러닝의 유형
(출처: Deep Learning Research Review: Reinforcement Learning)
이전에 다룬 ConvNet, RNN/LSTM 등은 모두 지도 학습(Supervise Learing) 또는 비지도 학습(Unsupervised Learning) 방법에 포함된다. 강화학습은 이와는 전혀 다른 머신러닝 방법으로, 일련의 "액션(action)"을 하고 "보상(reward)"을 받는 과정을 통해, 미래의 수행할 액션에 대한 최적의 "의사결정(decision process)"을 내리는 방법을 학습한다.
스스로 배우기: 공받기 게임
시작하기 전에
감을 잡기 위해 먼저 동작하는 코드를 보여준다. 이 글에서 소개하는 Torch 기반 과일 받기 게임 예제는 Sean Naren이 작성한 QlearningExample.torch 프로젝트를 가져다 썼다. 그리고 해당 코드는 Eder Santana가 케라스(Keras)를 이용해서 작성한 코드를 기반으로 만들어졌다. 그리고 이 코드는 Nervana가 쓴 강화학습과 DQN에 대한 소개 글인 "Guest Post (Part I): Demystifying Deep Reinforcement Learning"에서 시작했다. 시간이 된다면 원문을 소개 글부터 시작해서 거꾸로 읽다보면 강화학습을 이해하는데 도움이 되리라고 본다. 이 글은 앞의 글들을 좀더 요약해서 간단히 설명하는 수준이다.
설치하기
먼저 Torch와 이미지 처리를 위한 qtlua를 설치한다. Torch를 설치하는 방법은 "Torch와 OpenCV를 활용한 실시간 이미지 분류 데모"의 "Torch 설치하기"를 참고한다. 여기에 추가로 이미지 처리를 위해 qtlua를 설치한다. 먼저 qtlua가 설치되어 있는지 확인한다.
1 2 3 4 5 6$ luarocks list qtlua Warning: Failed loading manifest for /Users/socurites/.luarocks/lib/luarocks/rocks: /Users/socurites/.luarocks/lib/luarocks/rocks/manifest: No such file or directory Installed rocks: ---------------- qtlua scm-1 (installed) - /Users/socurites/Git/Torch/distro/install/lib/luarocks/rocks
만약 설치가 되어 있지 않다면 아래와 같이 설치한다.
1$ luarocks install qtlua
qtlua는 qt 라이브러리를 기반으로 하므로, qt가 설치되어 있어야 한다. 유의할 점은 최신 버전인 qt 5.X 버전은 qtlua에서 지원하지 않으며, qt 4.X 버전만을 지원한다. Mac을 사용한다면 4.X 버전의 qt를 설치한 후, brew switch 명령을 사용하여 버전을 변경한다.
의존성이 필요한 추가 패키지가 있으면 유사한 방법으로 설치한다. 딥러닝을 위한 optim과 이미지 처리를 위한 image 패키지도 필수로 설치해야 한다.
QlearningExample.torch 프로젝트를 fork하여 만든 QlearningExampleKoreanExplained.torch 프로젝트를 로컬로 클론한다.
1$ git clone https://github.com/socurites/QlearningExampleKoreanExplained.torch.git
학습하기
1000 에폭만큼 학습한다.
1 2 3 4 5 6 7 8$ th Train.lua -epoch 1000 Epoch 1 : err = 0.052809 : Win count 0 Epoch 2 : err = 0.268234 : Win count 1 ... Epoch 998 : err = 0.050666 : Win count 519 Epoch 999 : err = 0.085724 : Win count 519 Epoch 1000 : err = 0.098179 : Win count 520 Model saved to TorchQLearningModel.t7
에폭이 진행될 때 마다 에러(err)는 감소하고, 승리 횟수(Win count)는 점진적으로 증가한다. 최종적으로 TorchQlearningModel.t7 모델 파일이 생성된다.
Bug Fixed
눈치가 있는 사람이라면, 승수(Win count)는 증가하는데 반해, 에러(err)은 변함이 없다는 사실을 눈치챘을 것이다. Sean Naren이 작성한 QlearningExample.torch 프로젝트의 학습 코드(Train.lua)에는 버그가 있다. 원본 코드의 82번째 라인 부분은 다음과 같다.
1 2 3local target = model:forward(memoryInput.inputState) --Gives us Q_sa, the max q for the next state. local nextStateMaxQ = torch.max(model:forward(memoryInput.nextState), 1)[1]
Q-learning을 위한 목표 Q값을 계산하기 위한 코드로, model:forward를 2번 호출하게 된다. Torch의 버그인지 모르겠으나, model:forward를 호출하여 그 결과값을 target에 할당한 이후, nextStateMaxQ를 계산하기 위해 model:forward를 호출하고 나면, target 값도 함께 변경된다(할당문이 없음에도). 정상적으로 학습하기 위해서는 82번째 라인을 아래와 같이 수정한다.
1local target = model:forward(memoryInput.inputState):clone()
변경된 Train.lua 파일을 이용하여 학습한 결과 로그는 다음과 같다.
1 2 3 4 5 6 7 8 9 10 11$ th Train.lua Epoch 1 : err = 0.025329 : Win count 0 Epoch 2 : err = 0.237292 : Win count 0 Epoch 3 : err = 0.239530 : Win count 1 ... Epoch 996 : err = 0.000018 : Win count 868 Epoch 997 : err = 0.000024 : Win count 869 Epoch 998 : err = 0.000022 : Win count 870 Epoch 999 : err = 0.000028 : Win count 871 Epoch 1000 : err = 0.000028 : Win count 872 Model saved to TorchQLearningModel.t7
에폭이 증가할 때마다 에러가 줄어들고, 승수도 수정 전의 학습 코드보다 더 빨리 증가한다.
시각화하기
학습된 모델을 사용하여 컴퓨터 스스로 과일 받기 게임을 수행하는 모습을 시각화해 본다.
1$ qlua TorchPlaysCatch.lua
아래 그림과 같이 스스로 과일 받기를 수행하는 모습을 확인할 수 있다.
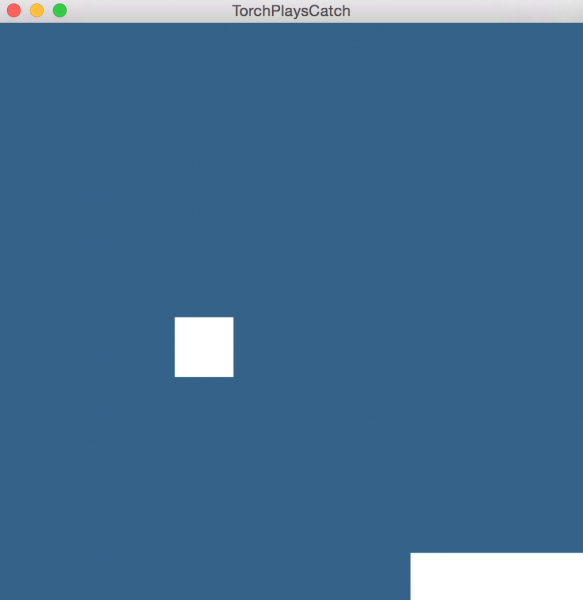
그림. 컴퓨터 스스로 과일 받기 게임을 하는 모습
강화학습에 대해
강화학습에 대한 내용은 Guest Post (Part I): Demystifying Deep Reinforcement Learning에 설명된 내용을 요약했으며, 모두의 연구소 이웅원님이 쓰신 Fundamental of Reinforcement Learning도 참고했다.
로드맵
Guest Post (Part I): Demystifying Deep Reinforcement Learning에서 강화학습을 설명하는 로드맵은 다음과 같다.
- 강화 학습에서 풀어야 할 문제 credit assignment 문제 exploration-exploitation 문제
- 강화학습 알고리즘을 수식으로 표현하는 방법 MDP(Markov Decision Process)
- 장기간에 걸친 전략을 정의하는 방법 discounted future reward
- future reward를 추정 또는 근사하는 방법 간단한 테이블 기반의 Q-learning 알고리즘
- 테이블이 너무 큰 경우 해결 방법 DQN(Deep Q Network)
- 실제로 동작하도록 만드는 추가 알고리즘들 experience replay
- epsilon-greedy exploration exploration-exploitation 문제를 해결하는 방법
강화학습
먼저 강화학습을 간략히 도식화한 아래 그림을 보자.
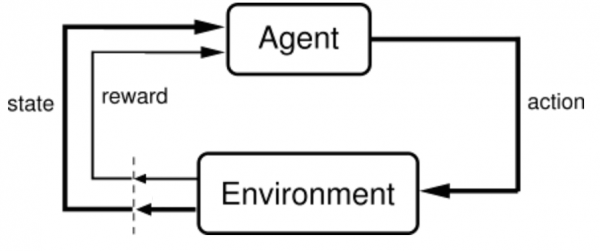
그림. 강화학습 구조
(출처: The Agent-Environment Interface)
에이전트(agent)는 현재 상태(state)의 환경(enviroment)에서 학습을 수행하는 또는 의사결정을 내리는 주체다. 에이전트는 의사결정에 따라 액션(action)을 수행한다. 액션에 따라 환경은 또 다른 상태로 변경되며, 에이전트에게는 보상(reward)을 제공한다.
예를 들어 과일 받기 게임의 경우 에이전트는 맨 아래에서 과일을을 받는 가로 3픽셀의 블록(또는 블록을 움직이는 주체)이며, 1프레임에서 블록이 취할 수 있는 액션은 왼쪽 1칸 이동, 오른쪽 1칸 이동 또는 그대로 있기 3가지다. 블록이 취한 액션에 따라 블록은 이동하며, 맨 위에서 떨어지는 과일은 아래로 1칸 이동하는 방식으로 환경의 상태는 변경된다. 또한 블록이 과일을 받는 경우(또는 가로/세로 1픽셀의 공이 가로 3픽셀의 블록과 겹치는 경우), 1점의 보상이 제공된다. 이 예제의 강화학습에서 에이전트는 최대한 많은 점수를 획득할 수 있는 의사결정 방법을 학습해야 한다.
credit assignment 문제
문제는 블록이 점수를 받기 직전에 한 액션은 보상과 직접적인 관련이 없다는 점이다. 예를 들어 과일이 가장 우측에서 내려오고 있고, 블록은 중앙에서 시작해서 우측으로 이동한 후 움직이지 않고 그 위치에 그대로 있는 경우를 생각해 보자. 이 경우 1점의 보상이 주어진다. 이때 보상 직전의 액션, 즉 "그대로 있기"보다는 과거의 중앙에서 우측으로 이동하는 일련의 액션들로 인해 획득한 보상이다. 이처럼 보상이 발생한 시점 이전의 일련의 액션들 중 보상에 기여한 액션들이 무엇인지, 또는 어느 단계까지 고려해야 하는지가 문제가 된다. 이를 credit assignment 문제라고 부른다.
exploration-exploitation 문제
에이전트가 일련의 액션을 통해 어느 수준의 보상을 획득하는 전략을 학습했다고 가정하자. 예를 들어 과일이 우측에서 시작하는 경우, 블록을 우측으로 이동후 "그대로 있기" 전략을 취한다고 해보자. 이 경우 최소한 1점의 보상을 얻게 되고, 운 좋게 과일이 연속으로 우측에서 시작된다면 2점을 획득할 수도 있다. 최소 1점을 얻는 이 전략에 만족할 것인지 아니면 더 나은 새로운 전략을 시도해볼 것인지에 대한 문제가 exploration-exploitation 문제다. 인간으로 치자면, 태어나서 "기는" 액션을 통해 움직이는 전략을 배우게 되지만, 자라면서 "걷는" 액션을 지속적으로 시도함으로써 더 나은 이동 전략을 학습하게 된다. 문제는 언제 그리고 얼마만큼 새로운 시도를 하느냐다.
Markov Decision Process
강화학습 알고리즘에서 액션(action)을 수행하는 에이전트(agent)는 어떤 환경(environment)안에 존재한다. 환경은 특정 상태(state)에 있으며, 에이전트가 액션을 수행함으로써 환경은 다른 상태로 전이하며, 특정 경우에 액션은 보상(reward)을 받는다. 그리고 액션은 변경된 상태에서 또다시 다른 액션을 수행하게 된다.
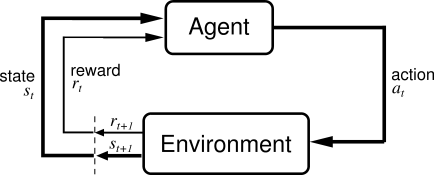
그림. 강화학습 구조
(출처: 3.1 The Agent-Environment Interface, Introduction to Reinforcement Learning, 2nd)
환경은 확률적(stochastic)이며, 이는 액션을 수행한 후 환경이 전이되는 상태와 보상은 랜덤하다는 뜻이다. 특정 상태에서 수행할 액션을 선택하는 규칙을 정책(policy)라고 부른다. 이러한 강화학습 알고리즘은 MDP(Markov Decision Process)를 이용하여 수식화 할 수 있다. 아래는 MDP 예다.
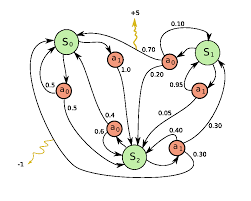
그림. MDP(Markov Decision Process)
따라서 MDP는 상태들의 집합 S, 액션들의 집합 A, 상태간 전이 확률 P, 보상 함수 R로 구성된다. Finite MDP는 유한 상태 시퀀스로 표현할 수 있다.
![]()
MDP에서 다음 상태와 보상은 현재 상태와 액션에만 의존성을 가진다. 위와 같은 시퀀스에서 다음에 받을 보상과 환경이 전이할 다음 상태는 아래와 같이 확률로 표현할 수 있다.
![]()
MDP의 경우 다음 상태와 보상은 현재 상태와 액션에만 의존성을 가지므로, 다음에 받을 보상과 환경이 전이할 다음 상태는 다음과 같다.
![]()
이처럼 다음 상태와 보상은 현재 상태와 액션에만 의존성을 가지는 경우 상태는 Markov 특성을 가진다라고 말한다.
Discounted Future Reward
에이전트가 수행할 액션 전략(policy)를 학습하는 과정은 현재 상태의 보상을 최대화하는 것이 아닌, 게임 장기간에 걸친 전체 보상을 최대화하는 방법을 학습하는 과정이다. 하나의 게임을 수행한 경우 아래와 같은 에피소드가 나온다고 해보자.
![]()
이 경우 전체 보상(total reward) R은 다음과 같다.
![]()
그리고 현재 시간 프레임 t에서 미래에 획득할 전체 보상(total future reward)은 다음과 같다.
![]()
반면 환경은 확률적(stochastic)이므로, 에피소드의 동일한 액션들을 다음에 수행했을 때 동일한 보상을 받을지 알 수 없다. 그리고 현재 1의 보상을 받는 액션을 수행하는 것이, 미래에 동일한 1의 보상을 받는 액션을 수행하는 것보다 더 낫다고 볼 수 있다. 따라서 미래의 보상은 시간이 지날수록 가치를 감소시키는 것이 합리적이다. 이러한 관점에서 현재 시간 프레임 t의 미래 보상은 discount factor를 아래와 같이 고려하며, 이를 discounted future reward라고 부른다. discount factor는 0과 1사이의 값이다
![]()
![]()
discount factor가 1인 경우, discounted future reward와 total future reward는 동일하다. 따라서 이 경우 환경은 확률적(stochastic)이 아닌 결정적(deterministic)이다. 반면 discount factor가 0인 경우, discounted future reward는 현재의 보상에만 의존한다. 따라서 discounted factor는 보통 0.9 정도의 값을 갖도록 한다.
강화학습의 목적은 (discounted) future reward를 최대로 하는 액션 선택 규칙, 즉 정책(policy)를 찾는 일이다. 참고로 Deepmind의 David Silver교수님이 쓰신 강화학습 강의인 UCL Course on RL에서 MDP는 아래와 같이 정의한다.

그림. MDP의 정의
테이블 기반의 Q-learning
먼저 아래와 같이 Q함수를 정의하자.
![]()
Q 함수는 상태 s에서 액션 a를 수행하고, 이어서 "최적"의 규칙에 따라 액션을 수행할 때 미래에 예상되는 전체 보상 discounted future reward의 최대 값을 나타낸다. 다시 말해 Q 함수는 상태 s에서 액션 a를 수행한 후, 일련의 액션이 지나 게임이 종료될 때 가질 수 있는 최고 점수라고 볼 수 있다.
정책(policy)
우선 위와 같이 정의한 Q 함수가 있다고 가정하자. 그리고 에이전트가 어떤 상태 s에 있고, 이 상태에서 취할 수 있는 액션 a와 b가 있다고 해보자. 이 중 어느 액션을 선택할지는 게임이 끝났을 때 어느 경우에 최종 점수가 높은지에 따라 달려 있다. 다시 말해 가장 높은 Q함수값을 가지는 액션들을 선택하면 된다. 그리고 각 상태 s에 대해 Q함수값이 가장 높은 액션들을 선택하는 규칙을 정책(policy)라고 부른다.
![]()
Bellman equation
일단 Q 함수가 있다고 가정하면, Q함수가 최고값을 가지는 액션들의 규칙, 즉 정책을 찾을 수 있다. 그리고 이러한 최적의 정책을 찾는 것이 강화학습의 목적이다. 이제 질문은 위의 정의를 만족하는 Q함수가 존재하느냐와 어떻게 계산하느냐다. 앞에서 설명한 Q함수의 정의는 재귀적이다.
- Q함수는 "최적"의 규칙에 따라 액션을 수행할 때 예상되는 미래 보상의 최대값이다.
- "최적"의 규칙, 정책을 따르면 최고값을 가지는 Q함수가 된다.
즉 Q함수는 "최적"의 규칙을 정의하는 함수이면서, "최적"의 규칙이란 Q함수가 최대값을 가지게 되는 액션들의 집합이다. 예를 들어 에피소드에서 아래의 전이 과정을 보자.
![]()
이 경우 Q함수는 아래와 같이 정의할 수 있다.
![]()
즉 Q함수는 현재 상태의 최고 보상 r과 다음 상태에서의 미래 보상의 최대값의 합이다. 위의 정의를 Bellman equation이라고 부른다.
Q-learning 알고리즘
Q-learning의 핵심은 Bellman equation을 반복적으로 사용하여 Q함수를 근사할 수 있다는 점이다. 가장 간단한 방법은 행렬 형태를 사용하는 것으로, 각 행은 상태( state)에 해당하며, 각 열은 액션(action)에 대응하며, 행렬 요소의 값은 Q함수가 가지는 값 Q(s, a)다. 이와 같은 행렬 형태를 사용하는 경우 Q함수는 아래와 같이 반복적으로 계산하여 근사할 수 있다.

그림. 테이블 형태의 Q-learning 알고리즘
(출처: Guest Post (Part I): Demystifying Deep Reinforcement Learning)
- 먼저 Q(s, a) 행렬을 랜덤값으로 초기화한다.
- 초기 상태 s에서 시작한다.
- 아래 과정을 반복적으로 수행한다.
- 액션 a를 선택하여 실행한다.
- 액션에 따른 보상 r과 변경된 상태 s'를 확인한다.
- Q값을 갱신한다.
- 현재 상태를 변경한다.
Q값은 아래의 수식을 따라 갱신한다. 참고로 알파는 일반적인 학습률(learning rate)에 해당한다.
![]()
알파가 1인 경우, 수식은 Bellman equation가 완전히 동일하다.
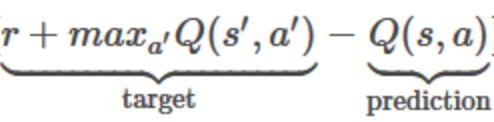
수식 우측의 Q(s, a)는 현재 임의로 초기화된 Q함수 값, 즉 알고리즘이 예측한 Q함수값이다. 수식 좌측은 실제 Q함수의 값으로 예측을 통해 찾으려는 값이다. 즉 실제값과 예측값의 차이를 손실 또는 에러로 사용하여 Q함수를 반복적으로 근사하게 된다.
DQN(Deep Q Network)
이러한 행렬 형태의 Q-learning 알고리즘의 문제는 사이즈(size)다. 행렬의 행은 상태(state)이며, 열은 액션(action)이다. 예를 들어 게임 화면의 사이즈가 84x84이고, 각 셀(cell)이 256개의 grayscale로 표현할 수 있다고 해보자. 그리고 게임 진행의 마지막 4프레임에 대해서 Q함수의 행렬을 계산하는 경우, 총
![]()
개의 상태, 즉 Q함수 행렬의 행 개수가 존재한다.
ConvNet과 같은 신경망(neural network)을 이용하면 이러한 고차원의 데이터를 쉽게 표현할 수 있다. 예를 들어 상태(게임의 마지막 4프레임 이미지)와 액션을 입력으로 받아서, 해당 상태와 액션의 Q함수값을 출력하는 신경망을 아래와 같이 정의할 수 있다.
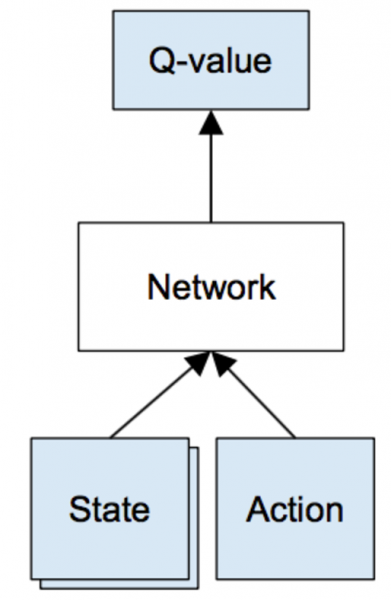
그림. Q-network: 신경망으로 표현한 Q-learning
(출처: Guest Post (Part I): Demystifying Deep Reinforcement Learning)
또는 상태(게임의 마지막 4프레임 이미지)만을 입력으로 받아서 한번의 피드포워드(FeedForward) 과정을 거쳐서, 각 액션별 Q함수값을 한꺼번에 출력하는 신경망을 정의할 수도 있다.
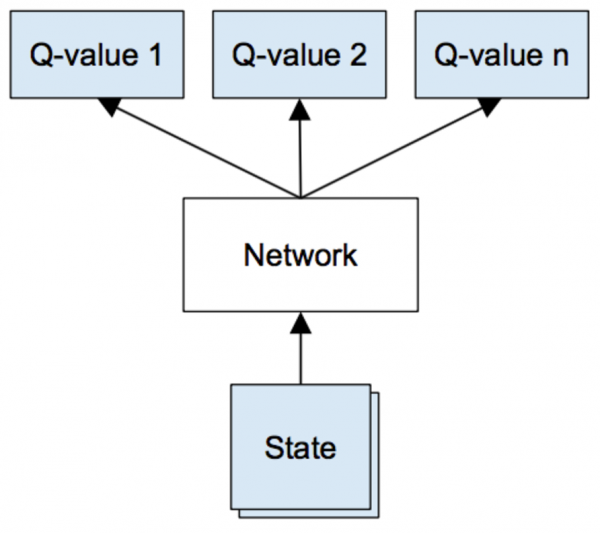
그림. Q-network(Deepmind 논문)
(출처: Guest Post (Part I): Demystifying Deep Reinforcement Learning)
그리고 신경망의 손실 함수(loss function)는 아래와 같이 제곱 오차(squared error)로 정의할 수 있으며, 이는 앞의 테이블 형태의 Q-learing 함수의 오차 정의와 거의 같다.
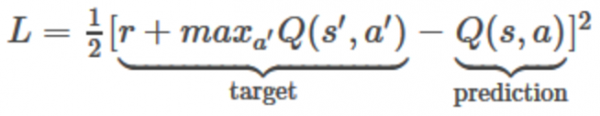
신경망을 사용하는 경우, 앞의 테이블 형태의 Q-learing 알고리즘에서 Q함수값을 갱신하는 과정을 아래와 같이 수정한다.
- 현재 상태 s에 대해 피드포워드 과정을 통과시켜, 모든 액션에 대한 모델의 Q예측값을 계산한다.
- 다음 상태 s'에 대해 피드포워드 과정을 통과시켜, 모델 출력값의 최대값, 즉 maxQ( s', a')를 계산한다.
- 현재 상태 s에 대한 액션 a에 대해서는 목표값을
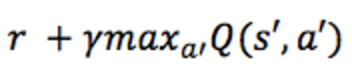
로 설정하고, 나머지 액션은 1번 과정에서 예측한 Q값을 목표값으로 설정한다(즉 나머지 액션에서는 에러가 0이다).
- 손실 함수를 계산 한후, backpropgation을 통해 파라미터를 업데이트한다.
Experience Replay
DQN 학습을 통해 Q함수를 근사하는 경우 지역 최소값(local minimum)에 빠지거나 발산하는 문제가 발생할 수 있다. 이러한 문제를 보완하는 방법이 experience replay 기법으로, 개념적으로는 미니배치(mini-batch)와 유사하다. 먼저 게임 과정의 전이 <s, a, r, s'>들을 모두 replay 메모리에 저장한다. 그리고 학습단계에서 최신 전이들을 하나씩 사용하는 대신, replay 메모리에서 랜덤으로 여러개를 선택해서 학습하는 방식이다.
epsilon-greedy exploration
Q-learning 알고리즘에서 초기 값(행렬 또는 네트워크 파라미터)는 모두 랜덤이다. 따라서 가장 높은 Q값을 가지는 액션을 선택한 경우, 액션 또한 랜덤으로 선택한 것과 같은 효과를 가지며, 에이전트는 exploration(탐험적인 활동)을 수행하게 된다. 반복적인 학습을 통해 Q함수가 수렴하게 되면, 이러한 탐험적인 액션은 줄어들게 된다. 이처럼 Q-learning 알고리즘 자체는 exploration 개념을 포함하고 있지만, 탐험적인 활동을 통해 최초 발견한 전략에서 벗어나지 못한다.
epsilon-greedy exploration은 이러한 문제를 해결하는 기법이다. 기본적으로는 가장 높은 Q값을 가지는 액션을 선택하고, 일정 확률(epsilon)로 랜덤으로 액션을 선택하도록 하는 방법이다. 딥마인드의 경우 학습이 진행되면서 epsilon의 값을 1에서 0.1로 점진적으로 감소시켰다. 따라서 학습 초기에는 랜덤으로 액션을 선택할 확률이 높고, 학습이 진행되어 Q함수가 수렴하게 되면 exploration(탐험적인 활동)은 고정된 비율로만 진행된다.
최종 DQN 알고리즘

그림. 최종 DQN 알고리즘
(출처: Guest Post (Part I): Demystifying Deep Reinforcement Learning)
- replay 메모리를 생성한다
- 신경망 파라미터를 랜덤으로 초기화한다.
- 초기 상태 s에서 시작한다.
- 아래 과정을 반복적으로 수행한다.
- epsilon-greedy exploration 기법에 따라 액션 a를 선택하여 실행한다.
- 일정 확률(epsilon)인 경우, 액션을 랜덤을 선택한다
- 아닌 경우, 가장 높은 Q값을 가지는 액션을 선택한다
- 액션에 따른 보상 r과 변경된 상태 s'를 확인한다.
- 경험 <s, a, r, s'>을 replay 메모리에 저장한다.
- replay 메모리에서 experience replay 기법에 따라 전이들의 미니배치를 랜덤으로 선택한다.
- 미니배치의 각 전이에 대해 목표 Q값을 계산한다.
- 변경된 상태가 터미널 상태(종료 상태)인 경우, 전이의 보상을 목표 Q값으로 할당한다
- 변경된 상태가 터미널 상태가 아닌 경우, Bellman equation을 따라 목표 Q값으로 계산한다
- 제곱 오차(squared error)를 신경망의 손실함수로 사용하여 Q-network를 학습시킨다(즉 네트워크 파라미터를 업데이트 한다)
- 현재 상태를 변경한다.
- epsilon-greedy exploration 기법에 따라 액션 a를 선택하여 실행한다.
Torch 학습 코드 뜯어 보기
지금까지 Q-learning과 신경망을 이용하여 Q-learning을 구현한 DQN 알고리즘에 대해 소개했다. 지금부터는 DQN 알고리즘을 실제로 어떻게 구현하는지에 대해 설명하고자 한다. 여기에서 설명하는 코드는 Sean Naren이 작성한 QlearningExample.torch 프로젝트를 기준으로 한다. 원본 학습 코드는 Train.lua에 있으며, DQN 알고리즘을 단계적으로 설명하기 위해 QlearningExampleKoreanExplained.torch에는 TrainConsole.lua를 추가로 작성했다.
먼저 Torch 콘솔을 열고, 필요한 패키지를 로드한다.
1 2 3 4$ th -- Load required packages require 'nn' require 'optim'
환경 정의
먼저 에이전트가 액션을 수행할 환경(enviroment)을 정의한다. 과일 받기 게임 환경에는 정방형의 격자 캔버스, 상단에서 떨어지는 과일, 그리고 과일을 받을 바구니로 구성된다. 게임이 보여지는 정방형의 캔버스의 크기는 고정되어 있으며, 환경에서 변화되는 요소는 과일의 좌표와 바구니의 좌표다. 따라서 환경이 변화되는 상태는 과일의 (x, y) 좌표와 바구니의 (x) 좌표로 구성된다(바구니의 y 좌표는 캔버스의 맨 하단으로 고정적이다).
1 2 3 4 5 6 7-- Initialise environment and state env = {} gridSize = 10 fruitRow = 1 fruitColumn = math.random(1, gridSize) basketPosition = math.random(2, gridSize - 1) state = torch.Tensor({ fruitRow, fruitColumn, basketPosition })
- gridSize 게임이 실행되는 캔버스의 격자 크기
- fruitRow 게임이 시작되면 과일은 최상단, 즉 1번째 행에 위치
- fruitColumn 게임이 시작되면 과일의 열(column) 위치는 랜덤하게 선택
- basketPosition 게임이 시작되면 바구니의 위치도 랜덤하게 선택. 단, 바구니는 가로가 3픽셀이므로, 바구니의 중심은 2부터 9사이에 위치
초기 상태(state)는 텐서 객체로 저장하며, 상태는 과일의 (x, y) 좌표와 바구니의 (x) 좌표로 구성된다.
캔버스(canvas)는 게임 실행 화면이며, 단순히 10(gridSize) x 10(gridSize) 크기의 텐서 객체로 생성할 수 있다. 기본값은 모두 0이며, 과일과 바구니가 위치하는 곳만 1을 할당한다.
1 2 3 4 5 6canvas = torch.Tensor(gridSize, gridSize):zero() canvas[state[1]][state[2]] = 1 -- Draw the fruit. -- Draw the basket. The basket takes the adjacent two places to the position of basket. canvas[gridSize][state[3] - 1] = 1 canvas[gridSize][state[3]] = 1 canvas[gridSize][state[3] + 1] = 1
게임이 시작된 상태의 캔버스는 다음과 같다.
1 2 3 4 5 6 7 8 9 10 11 12th> canvas 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 [torch.DoubleTensor of size 10x10]
이제 현재 상태의 캔버스를 현재 상태로 저장한다.
1currentState = canvas:clone()
신경망 정의
Q-network로 사용할 신경망을 정의한다.
1 2 3 4 5 6 7 8 9 10-- Create network nbStates = 100 hiddenSize = 100 nbActions = 3 model = nn.Sequential() model:add(nn.Linear(nbStates, hiddenSize)) model:add(nn.ReLU()) model:add(nn.Linear(hiddenSize, hiddenSize)) model:add(nn.ReLU()) model:add(nn.Linear(hiddenSize, nbActions))
신경망 모델은 1개의 은닉층을 가지는 fully-connected layer로 구성한다. 입력 레이어는 100개의 노드를 가지는데, 이는 10x10 크기를 가지는 캔버스가 입력이기 때문이다. 출력 레이어는 3개의 노드로 구성되며, 이는 선택할 수 있는 액션(왼쪽으로 이동, 그대로 있기, 오른쪽으로 이동)에 대응한다.
1 2 3 4 5 6 7 8 9th> model nn.Sequential { [input -> (1) -> (2) -> (3) -> (4) -> (5) -> output] (1): nn.Linear(100 -> 100) (2): nn.ReLU (3): nn.Linear(100 -> 100) (4): nn.ReLU (5): nn.Linear(100 -> 3) }
액션 선택
초기 상태에서 수행할 액션을 선택한다. 액션 선택시에는 epsilon-greedy exploration 기법을 적용하여, 일정 확률(epsilon)로 랜덤으로 액션을 선택하거나 또는 가장 높은 Q값을 가지는 액션을 선택하도록 한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18-- epsilon-greedy exploration: select action --[[ Helper function: Chooses a random value between the two boundaries.]] -- function randf(s, e) return (math.random(0, (e - s) * 9999) / 10000) + s; end epsilon = 1 if (randf(0, 1) <= epsilon) then action = math.random(1, nbActions) else q = model:forward(currentState) _, index = torch.max(q, 1) action = index[1] end -- Decay the epsilon by multiplying by 0.999, not allowing it to go below a certain threshold. epsilonMinimumValue = 0.001 if (epsilon > epsilonMinimumValue) then epsilon = epsilon * 0.999 end
또한 학습이 진행될 때마다 epsilon의 값을 1에서 0.01로 점진적으로 감소시킨다. 현재 선택된 액션은 3, 즉 오른쪽으로 1칸 이동하는 액션이다.
1 2th> action 3
액션에 따른 보상 r과 변경된 상태 s' 확인
선택된 액션에 따른 보상과 변경된 상태를 확인한다. 앞서 액션을 선택할 때 액션은 1(왼쪽으로 이동), 2(그대로 있기), 3(오른쪽으로 이동)에 해당한다. 반면 캔버스의 픽셀 이동 관점에서 액션은 -1(왼쪽으로 이동), 0(그대로 있기), 1(오른쪽으로 이동)에 해당한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14-- carry action on environment if (action == 1) then move = -1 elseif (action == 2) then move = 0 else move = 1 end -- observe new state fruitRow = fruitRow + 1 -- The min/max prevents the basket from moving out of the grid. basketPosition = math.min(math.max(2, basketPosition + move), gridSize - 1) fruitColumn = fruitColumn -- it's fixed state = torch.Tensor({ fruitRow, fruitColumn, basketPosition })
게임의 1프레임이 진행되면, 과일의 행(row)는 1 증가하고, 바구니는 선택한 액션에 따라 1칸씩 이동한다(이 경우는 오른쪽으로 1칸 이동한다). 그리고 과일의 열(column) 위치는 고정적이다. 변경된 상태를 텐서 객체로 생성한다.
이제 새로운 상태의 캔버스를 다음 상태로 저장한다.
1 2 3 4 5 6 7 8-- initialise canvas of next state canvas = torch.Tensor(gridSize, gridSize):zero() canvas[state[1]][state[2]] = 1 -- Draw the fruit. -- Draw the basket. The basket takes the adjacent two places to the position of basket. canvas[gridSize][state[3] - 1] = 1 canvas[gridSize][state[3]] = 1 canvas[gridSize][state[3] + 1] = 1 nextState = canvas:clone()
nextState를 출력해 보면, 과일은 2행으로 이동했고, 바구니는 오른쪽으로 1칸 이동했음을 확인할 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12th> nextState 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 [torch.DoubleTensor of size 10x10]
액션에 따른 보상을 확인한다. 보상은 과일이 바구니 위로 온 경우다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15-- observe reward reward = 0 if (fruitRow == gridSize - 1) then -- If the fruit has reached the bottom. if (math.abs(fruitColumn - basketPosition) <= 1) then -- Check if the basket caught the fruit. reward = 1 else reward = -1 end else reward = 0 end winCount = 0 gameOver = false if (reward == 1) then winCount = winCount + 1 end if (nextState[1] == gridSize - 1) then gameOver = true end
경험 <s, a, r, s'>을 replay 메모리에 저장
현재까지 진행한 게임 전이를 replay 메모리에 저장한다.
1 2 3 4 5 6 7 8 9 10-- Initialise replay memory memory = {} -- save an experience to replay memory table.insert(memory, { inputState = currentState:view(-1), action = action, reward = reward, nextState = nextState:view(-1), gameOver = gameOver });
experience replay 기법에 따라 전이들의 미니배치를 랜덤으로 선택
replay 메모리에 저장된 전이들의 미니배치를 랜덤으로 선택한다. 현재는 1개의 전이만 replay 메모리에 저장되어 있는 상태다.
1 2 3 4 5 6 7 8 9 10-- choose mini-batch of transitions batchSize = 50 memoryLength = #memory chosenBatchSize = math.min(batchSize, memoryLength) inputs = torch.Tensor(chosenBatchSize, nbStates):zero() targets = torch.Tensor(chosenBatchSize, nbActions):zero() i = 1 -- Choose a random memory experience to add to the batch. randomIndex = math.random(1, memoryLength) memoryInput = memory[randomIndex]
미니배치의 각 전이에 대해 목표 Q값을 계산
미니배치의 각 전이에 대해 목표 Q값을 계산한다. 앞에서 설명한 DQN 알고리즘에서 Q값을 계산하는 방법은 다음과 같다.
- 변경된 상태가 터미널 상태(종료 상태)인 경우, 전이의 보상을 목표 Q값으로 할당한다
- 변경된 상태가 터미널 상태가 아닌 경우, Bellman equation을 따라 목표 Q값으로 계산한다
그리고 Bellman equation에 따라 목표 Q값을 계산하는 방법은 다음과 같다.
- 현재 상태 s에 대해 피드포워드 과정을 통과시켜, 모든 액션에 대한 모델의 Q예측값을 계산한다.
- 다음 상태 s'에 대해 피드포워드 과정을 통과시켜, 모델 출력값의 최대값, 즉 maxQ( s', a')를 계산한다.
- 현재 상태 s에 대한 액션 a에 대해서는 목표값을
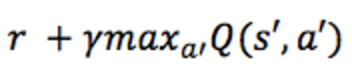
로 설정하고, 나머지 액션은 1번 과정예 예측한 Q값을 목표값으로 설정한다(즉 나머지 액션에서는 에러가 0이다).
- 손실 함수를 계산 한후, backpropgation을 통해 파라미터를 업데이트한다.
Torch 로 구현하면 다음과 같다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16-- Calculate Q-value if (memoryInput.gameOver) then target[memoryInput.action] = memoryInput.reward else -- Gives us Q_sa for all actions target = model:forward(memoryInput.inputState):clone() -- reward + discount(gamma) * max_a' Q(s',a') -- We are setting the Q-value for the action to r + γmax a’ Q(s’, a’). -- The rest stay the same to give an error of 0 for those outputs. -- the max q for the next state. nextStateMaxQ = torch.max(model:forward(memoryInput.nextState), 1)[1] target[memoryInput.action] = memoryInput.reward + discount * nextStateMaxQ end -- Update the inputs and targets. inputs[i] = memoryInput.inputState targets[i] = target
먼저 모든 액션에 대한 Q값을 계산한다.
1 2 3 4 5 6 7 8th> target = model:forward(memoryInput.inputState) [0.0002s] th> target 0.01 * 2.9141 -6.1104 -2.8024 [torch.DoubleTensor of size 3]
그리고 입력 상태의 액션(이 경우 3)에 대해서는 Bellman equation에 따라 Q값을 변경한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16th> nextStateMaxQ = torch.max(model:forward(memoryInput.nextState), 1)[1] [0.0002s] th> memoryInput.action 3 [0.0001s] th> target[memoryInput.action] = memoryInput.reward + discount * nextStateMaxQ [0.0000s] th> memoryInput.reward + discount * nextStateMaxQ 0.036374518976032 [0.0001s] th> target 0.01 * 2.9141 -6.1104 3.6375 [torch.DoubleTensor of size 3]
보는 것과 같이 목표 Q값 중 3번째 항목의 값만 갱신되었다. 따라서 나중에 Q-network를 학습할 때 나머지 액션에 대해서는 에러가 0이 된다.
Q-network를 학습
Q-network를 학습한다. Torch에서 딥러닝을 구현하는 방법을 그대로 따르며, 예제에서는 optim 패키지의 sgd 메서를 활용했다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22-- Train the network which returns the error. criterion = nn.MSECriterion() sgdParams = { learningRate = 0.1, learningRateDecay = 1e-9, weightDecay = weightDecay, momentum = 0.9, dampening = 0, nesterov = true } loss = 0 x, gradParameters = model:getParameters() function feval(x_new) gradParameters:zero() local predictions = model:forward(inputs) local loss = criterion:forward(predictions, targets) local gradOutput = criterion:backward(predictions, targets) model:backward(inputs, gradOutput) return loss, gradParameters end _, fs = optim.sgd(feval, x, sgdParams) loss = loss + fs[1]
코드에서 보는 것처럼 MSECriterion을 사용하여 아래의 목표 Q값(target)과 네트워크의 예측값(prediction)간의 에러를 계산한다.
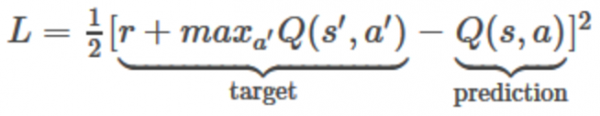
반복적으로 학습하기
이제 앞의 과정을 반복적으로 수행하여 Q-network를 학습한다. 원본 학습 코드 Train.lua에는 지금까지 설명한 내용을 객체지향적으로 구현되어 있다. 환경(enviroment)는 CatchEnviroment.lua에 환경과 상태 관련 모듈이 구현되어 있으며, replay memory 객체는 Train.lua 내부에 Memory 함수로 구현되어 있다. 앞서 설명한 내용을 바탕으로 Train.lua를 읽는다면 크게 어렵지 않을 것이다.
다음에는
이번 글의 목표는 이론적인 부분에 대해 깊이 이해하기보다 동작하는 코드를 기반으로 강화학습에 대해 개념을 잡는 것으로 목표를 정했다. 다음에 기회가 된다면 Deepmind의 David Silver교수님이 쓰신 강화학습 강의인 UCL Course on RL를 공부한 후 소개하는 글을 써 보고자 한다.
참고자료
- Deep Learning Research Review: Reinforcement Learning
- 모두의 연구소, Fundamental of Reinforcement Learning
- Github, QlearningExample.torch
- Keras plays catch, a single file Reinforcement Learning example
- Guest Post (Part I): Demystifying Deep Reinforcement Learning
- Torch와 OpenCV를 활용한 실시간 이미지 분류 데모
- Github, QlearningExampleKoreanExplained.torch
- UCL Course on RL
- Decision Process
- Shutton & Barton, "Introduction to Reinforcement Learning, 2nd"






