개요

이번 포스팅에는 R에서 사용하는 기초통계 관련 함수들을 알아본다.

해당강의에서는 기초통계학의 내용은 다루지 않고 기초통계학에서 사용하는 기법들을 R에서 어떻게 적용하는지 다룬다. 다만 참고를 위해 기초 통계학개념에 대해서는 위키피디아에서 발췌하여 추가해두었다.

코드중심의 설명이기 때문에 본문 보다는 코드의 주석이 집중적으로 추가되어 있으니 참고 바란다.

이번시간에 배울것들 요약

이번시간에는 아래와 같은 통계 지표들을 구하는 함수들에 대해 배워본다.

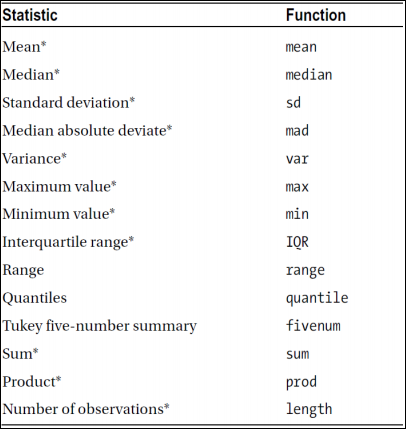
기초 통계 함수들

attach / detach

attach() 함수는 R 검색경로에 데이터프레임을 추가하는 것이고 detatch()는 그 반대이다.

쉽게 설명하면 통계 함수 등을 쓸 때 매번 데이터프레임명을 입력하는 것이 번거롭기 때문에 attach기능을 이용하여 데이터프레임명을 생략하는 방법이다.

코드 예제로 살펴보자.

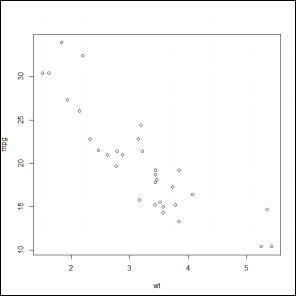
1
2
3
4
5
6
7
8
9
10
11
> summary(mtcars$mpg) # mtcars의 mpg의 요약을 조회한다.
Min. 1st Qu. Median Mean 3rd Qu. Max.
10.40 15.42 19.20 20.09 22.80 33.90
> plot(mtcars$wt, mtcars$mpg) # mtcars의 wt, mpg로 차트를 그려본다.
This could also be written as
> attach(mtcars) # mtcars를 attach한다.
> summary(mpg) # attach이후부터는 데이터프레임명을 생략 할 수 있다.
Min. 1st Qu. Median Mean 3rd Qu. Max.
10.40 15.42 19.20 20.09 22.80 33.90
> plot(wt, mpg)
> detach(mtcars)

차트를 그려보면 아래와 같은 차트가 나온다.

평균값(Mean)

평균값을 계산하는 것으로 입력값을 벡터로 선택한다.

mean() 함수는 기본적으로 컬럼 1개에 대한 계산을 수행하고 colMeans()는 여러개의 컬럼의 평균을 계산하기 위해 사용한다.

1
2
3
4
5
6
7
8
9
10
11
12
> attach(mtcars)
> mean(mpg) # 단순 평균 계산
[1] 20.09062
> mean(mpg, trim=0.05) # 절삭평균을 사용할때  trim값을 0~0.05로 지정
[1] 19.95333
> mean(mpg, trim=0.1) # 절삭평균을 사용할때  trim값을 0~0.1로 지정
[1] 19.69615
> detach(mtcars)
> vars <- c("mpg", "hp", "wt")
> colMeans(mtcars[vars]) # 컬럼의 평균을 한번에 뽑아준다.
      mpg        hp        wt
 20.09062 146.68750   3.21725

중위수(Median), 분위수(Quantiles)

중위수(Median)와 분위수(Quantile)을 구하는 법을 알아보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
> attach(mtcars)
> median(mpg)
[1] 19.2
> quantile(mpg, probs=c(0.1, 0.5, 0.9)) # probs 옵션으로 벡터형식으로 지정해주면 원하는 퍼센트의 분위수를 구할 수 있다.
  10%   50%   90%
14.34 19.20 30.09
> detach(mtcars)
> vars <- c("mpg", "hp", "wt")
> apply(mtcars[vars], 2, median) # apply함수를 활용하여 칼럼별 중위값을 구할 수 있다. 문법은 apply(대상값, 칼럼값, 함수, 옵션값)이다.
    mpg      hp      wt
 19.200 123.000   3.325
> apply(mtcars[vars], 2, quantile) # 마찬가지로 qunatile도 복수의 컬럼으로 구할 수 있다.
        mpg    hp      wt
0%   10.400  52.0 1.51300
25%  15.425  96.5 2.58125
50%  19.200 123.0 3.32500
75%  22.800 180.0 3.61000
100% 33.900 335.0 5.42400

최빈값(Mode)

통계의 Mode(최빈값)을 구하는 방법을 알아보자. 하지만 R은 빌트인 함수로는 mode를 제공하지 않는다. 따라서 Mode값을 조회해 보기 위해 크게 2가지 방법이 있다.

table함수와 sort함수를 조합해서 찾아보기 prettyR패키지 설치하여 Mode함수 사용하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
> attach(mtcars)
> table(cyl) # 실린더 개수는 전체 데이터셋에서 4개, 6개, 8개만 존재한다. table함수 실행 시 실런더가 4개, 6개, 8개일때 빈도가 11, 7, 14라는 내용을 출력한다.
cyl
4 6 8
11 7 14
> sort(table(cyl)) # sort함수를 조합하면 빈도순으로 정렬하여 출력한다.
cyl
6 4 8
7 11 14
> detach(mtcars)
> # install.packages("prettyR") # 옵션으로 prettyR을 설치하면 Mode함수를 사용할 수 있다. 대문자 Mode가 prettyR 패키지에 존재하는 함수이다.
> library(prettyR)
> Mode(mtcars$cyl)
[1] "8"

표준점수

표준점수를 구하는 방법을 알아보자. scale() 함수를 사용하여 표준점수를 구할 수 있다.

표준점수 = ()원 점수 - 평균 점수) / 표준편차

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
> zmpg <- scale(mtcars$mpg)
> zmpg
             [,1]
 [1,]  0.15088482
 [2,]  0.15088482
 [3,]  0.44954345
 [4,]  0.21725341
 [5,] -0.23073453
 [6,] -0.33028740
 [7,] -0.96078893
 [8,]  0.71501778
 [9,]  0.44954345
[10,] -0.14777380
[11,] -0.38006384
[12,] -0.61235388
[13,] -0.46302456
[14,] -0.81145962
[15,] -1.60788262
[16,] -1.60788262
[17,] -0.89442035
[18,]  2.04238943
[19,]  1.71054652
[20,]  2.29127162
[21,]  0.23384555
[22,] -0.76168319
[23,] -0.81145962
[24,] -1.12671039
[25,] -0.14777380
[26,]  1.19619000
[27,]  0.98049211
[28,]  1.71054652
[29,] -0.71190675
[30,] -0.06481307
[31,] -0.84464392
[32,]  0.21725341
attr(,"scaled:center")
[1] 20.09062
attr(,"scaled:scale")
[1] 6.026948
> mean(zmpg)
[1] 7.112366e-17
> sd(zmpg) # 표준편
[1] 1

분산, 표준편차

분산은 var(), 표준편차는 sd()로 구할 수 있다.

통계적으로 분산은 제곱단위이기 때문에 원 데이터의 단위로 맞추기 위해 표준편차를 사용한다.

1
2
3
4
5
6
7
8
9
10
11
12
> attach(mtcars)
> var(mpg)
[1] 36.3241
> sd(mpg)
[1] 6.026948
> detach(mtcars)
> vars <- c("mpg", "hp", "wt")
> var(mtcars[vars]) # 여러 칼럼의 분산값은 왼쪽과 같은 문법으로 구할 수 있다.
            mpg         hp        wt
mpg   36.324103 -320.73206 -5.116685
hp  -320.732056 4700.86694 44.192661
wt    -5.116685   44.19266  0.957379

Range

Range()는 최대값과 최소값을 구해준다.

1
2
3
4
5
6
> attach(mtcars)
> range(mpg)
[1] 10.4 33.9
> max(mpg)-min(mpg)
[1] 23.5
> detach(mtcars)

Interquartile Range (IQR)

IQR은 4분위값(quantile 4개) = 3번째 분위값 - 1번째 분위값을 사용하는 것으로 중간의 50%값을 보기위해 사용한다.

1
2
> IQR(mtcars$mpg)
[1] 7.375

변동계수(Coefficient of Variation)

변동 계수(coefficient of variation)는 표준 편차를 산술 평균으로 나눈 것이다. 상대표준편차(relative standard deviation)라고도 한다. 측정단위가 서로 다른 자료를 비교하고자 할 때 쓰인다. 즉, 범위나 분산과 같은 산포도를 계산하는 것만으로는 충분하지 않아 상대적인 산포도를 비교해야 한다. 변동 계수의 값이 클수록 상대적인 차이가 크다는 것을 의미한다.

1
2
3
4
5
6
> attach(mtcars)
> sd(mpg)/mean(mpg)
[1] 0.2999881
> sd(wt)/mean(wt)
[1] 0.3041285
> detach(mtcars)

공분산(Covariance)

공분산(covariance)은 2개의 확률변수의 상관정도를 나타내는 값이다.(1개의 변수의 이산정도를 나타내는 분산과는 별개임) 만약 2개의 변수중 하나의 값이 상승하는 경향을 보일 때, 다른 값도 상승하는 경향의 상관관계에 있다면, 공분산의 값은 양수가 될 것이다. 반대로 2개의 변수중 하나의 값이 상승하는 경향을 보일 때, 다른 값이 하강하는 경향을 보인다면 공분산의 값은 음수가 된다. 이렇게 공분산은 상관관계의 상승 혹은 하강하는 경향을 이해할 수 있으나 2개 변수의 측정 단위의 크기에 따라 값이 달라지므로 상관분석을 통해 정도를 파악하기에는 부적절하다. 상관분석에서는 상관관계의 정도를 나타내는 단위로 모상관계수 ρ를 사용한다.

공분산은 보통 두변수가 같은 방향으로 움직이는지 알아보기 위해 사용한다.

사용법은 cov()함수를 이용하여 사용 할 수 있다.

1
2
3
4
> attach(mtcars)
> cov(wt, mpg)
[1] -5.116685
> detach(mtcars)

상관분석(Correlation Analysis)

상관분석(Correlation Analysis)은 확률론과 통계학에서 두 변수간에 어떤 선형적 관계를 갖고 있는 지를 분석하는 방법이다. 두변수는 서로 독립적인 관계로부터 서로 상관된 관계일 수 있으며 이때 두 변수간의 관계의 강도를 상관관계(Correlation)라 한다. 상관분석에서는 상관관계의 정도를 나타내는 단위로 모상관계수 ρ를 사용한다.

상관관계의 정도를 파악하는 상관계수(Correlation coefficient)는 두 변수간의 연관된 정도를 나타낼 뿐 인과관계를 설명하는 것은 아니다. 두 변수간에 원인과 결과의 인과관계가 있는지에 대한 것은 회귀분석을 통해 인과관계의 방향, 정도와 수학적 모델을 확인해 볼 수 있다.

사용법은 cor()함수를 이용하여 사용 할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
> attach(mtcars)
> cor(wt, mpg) # equivalent to cov(wt, mpg)/(sd(wt)*sd(mpg)) #wt와 mpg는 반대의 상관관계를 가지고 있다고 해석할 수 있다.
[1] -0.8676594
> detach(mtcars)
> vars <- c("mpg", "hp", "wt")
> cov(mtcars[vars]) # equivalent to var(mtcars[vars])
mpg hp wt
mpg 36.324103 -320.73206 -5.116685
hp -320.732056 4700.86694 44.192661
wt -5.116685 44.19266 0.957379
> cor(mtcars[vars])
mpg hp wt
mpg 1.0000000 -0.7761684 -0.8676594
hp -0.7761684 1.0000000 0.6587479
wt -0.8676594 0.6587479 1.0000000

비대칭도(Skewness), 첨도(Kurtosis)

비대칭도 또는 왜도(Skewness)는 실수 값 확률 변수의 확률 분포 비대칭성을 나타내는 지표이다. 왜도의 값은 양수나 음수가 될 수 있으며 정의되지 않을 수도 있다. 왜도가 음수일 경우에는 확률밀도함수의 왼쪽 부분에 긴 꼬리를 가지며 중앙값을 포함한 자료가 오른쪽에 더 많이 분포해 있다. 왜도가 양수일 때는 확률밀도함수의 오른쪽 부분에 긴 꼬리를 가지며 자료가 왼쪽에 더 많이 분포해 있다는 것을 나타낸다. 평균과 중앙값이 같으면 왜도는 0이 된다.

첨도(kurtosis)는 확률분포의 뾰족한 정도를 나타내는 척도이다. 관측치들이 어느 정도 집중적으로 중심에 몰려 있는가를 측정할 때 사용된다. 첨도값(K)이 0에 가까우면 산포도가 정규분포에 가깝다. 0보다 작을 경우에는(K<0) 정규분포보다 더 완만하게 납작한 분포로 판단할 수 있으며, 첨도값이 0보다 큰 양수이면(K>0) 산포는 정규분포보다 더 뾰족한 분포로 생각할 수 있다.

사용법은 psych 패키지 설치 후 skew(), kurtosi()로 사용하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
> attach(mtcars)
> n <- length(mpg)
> m <- mean(mpg)
> s <- sd(mpg)
> skew <- sum((mpg-m)^3/s^3)/n
> kurt <- sum((mpg-m)^4/s^4)/n-3
> detach(mtcars)
> skew
[1] 0.610655
> kurt
[1] -0.372766
> # install.packages("psych")
> library(psych)
> attach(mtcars)
> skew(mpg)
[1] 0.610655
> kurtosi(mpg)
[1] -0.372766
> detach(mtcars)

summary 함수

summary() 함수를 통해서 아래의 지표들을 구할 수 있다.

• minimum
• maximum
• quartiles
• the mean for numerical variables
• frequencies

1
2
3
4
5
6
7
8
9
> vars <- c("mpg", "hp", "wt")
> summary(mtcars[vars])
mpg hp wt
Min. :10.40 Min. : 52.0 Min. :1.513
1st Qu.:15.43 1st Qu.: 96.5 1st Qu.:2.581
Median :19.20 Median :123.0 Median :3.325
Mean :20.09 Mean :146.7 Mean :3.217
3rd Qu.:22.80 3rd Qu.:180.0 3rd Qu.:3.610
Max. :33.90 Max. :335.0 Max. :5.424

stat.desc 함수

pastecs 패키지의 stat.desc()를 이용하면 아래의 지표들을 구할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
> # install.packages("pastecs")
> library(pastecs)
> stat.desc(mtcars[vars])
mpg hp wt
nbr.val 32.0000000 32.0000000 32.0000000
nbr.null 0.0000000 0.0000000 0.0000000
nbr.na 0.0000000 0.0000000 0.0000000
min 10.4000000 52.0000000 1.5130000
max 33.9000000 335.0000000 5.4240000
...
SE.mean 1.0654240 12.1203173 0.1729685
CI.mean.0.95 2.1729465 24.7195501 0.3527715
var 36.3241028 4700.8669355 0.9573790
std.dev 6.0269481 68.5628685 0.9784574
coef.var 0.2999881 0.4674077 0.3041285

describe 함수

psych 패키지의 describe()함수를 사용하면 아래의 지표들을 한번에 구할 수 있다.

• 표본수
• mean
• standard deviation
• median
• trimmed mean
• median absolute deviation
• minimum
• maximum
• range
• skew
• kurtosis
• standard error of the mean

1
2
3
4
5
6
7
8
9
10
11
> # install.packages("psych")
> library(psych)
> describe(mtcars[vars])
vars n mean sd median trimmed mad min max
mpg 1 32 20.09 6.03 19.20 19.70 5.41 10.40 33.90
hp 2 32 146.69 68.56 123.00 141.19 77.10 52.00 335.00
wt 3 32 3.22 0.98 3.33 3.15 0.77 1.51 5.42
range skew kurtosis se
mpg 23.50 0.61 -0.37 1.07
hp 283.00 0.73 -0.14 12.12
wt 3.91 0.42 -0.02 0.17