[딮러닝/영상처리] Convolution & Correlation 이해하기
CNN과 영상처리에 대해서 공부하면서, Convolution에 대한 내용을 정리한 내용입니다.
제가 잘못 이해하고 있는 부분에 대해서는 언제든지 지적해주시면 감사하겠습니다.
1. Convolution & Correlation
1-1. Convolution, 합성곱
위키피디아에서 Convolution(영문)을 찾아보면 보면 정의는 다음과 같이 되어있습니다.
- 1D Convolution
- 2D Convolution
1-2. Correlation, 상관분석
수식 정의는 다음과 같습니다.
- 1D Correlation
- 2D Correlation
Convolution과 Correlation수식을 잘 보면, 단지 +와 -에 대한 차이밖에 없습니다. 그리고 만약 입력함수가 y축에 대칭적이라면 Convolution의 정의에 따라 입력함수가 좌/우 반전이 되더라도 입력함수의 모양은 같기 때문에 Convolution과 Correlation은 같게 됩니다. 하지만 Convolution과 Correlation을 사용하는 용도와 의미는 서로 다릅니다.
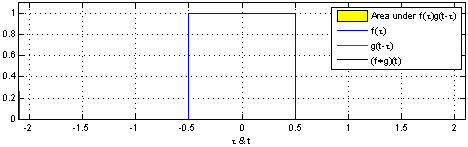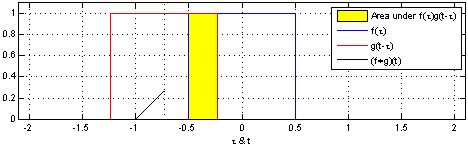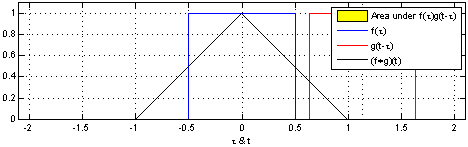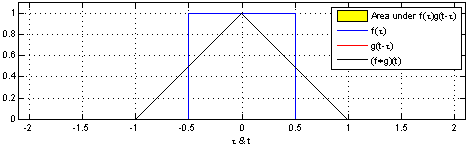
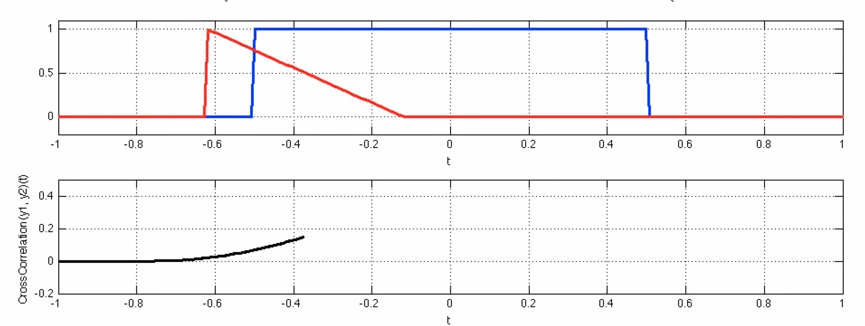
다음 위 영상은 Convolution과 Correlation에 대해서 아래의 Gif는 Convolution을 시각적으로 나타낸 것입니다.
|
Correlation
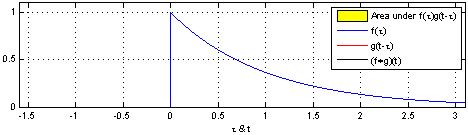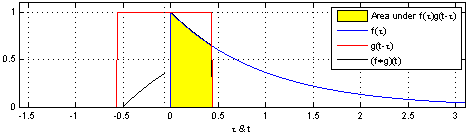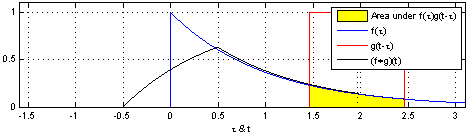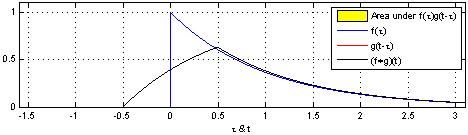
위의 영상을 보면, 입력함수(파란색)와 대상 함수 혹은 시스템 함수(빨간색)을 그대로 두고(좌/우 반전없이), 입력함수를 시간 축에 따라 움직이며(sliding), 대상 함수 혹은 시스템 함수와 겹치는 면적을 그래프로 나타냄을 알 수 있습니다.
 |
 |
|
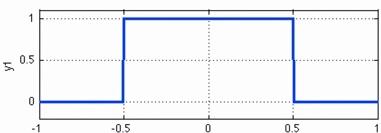
[ 입력 함수 ] |
[ 대상 함수 혹은 시스템 함수 ] |
[ Correlation 결과]
Correlation은 대상 함수 혹은 시스템함수와 입력함수가 똑같이 일치하는 시점에 오면 진폭의 높이가 최대값을 갖습니다. 즉, 입력 함수와 대상 함수 혹은 시스템 함수가 얼마나 유사한지에 대해서 측정할 수 있는 도구가 Correlation이 됩니다.
Correlation의 대표적인 사용 사례는 다음과 같습니다.
만약에 우리가 아래와 같은 어떤 전체 Image와 오른쪽에 작은 Patch의 Image를 받았다고 가정합니다. 여기서 우리가 알고싶은 것은 저 Full Image에서 작은 Patch Image가 이 Full Image에 속해있는 Image이면서, 위치가 어디인지 알고 싶을 때, Correlation 기법을 이용하여 구할 수 있습니다. 만약에 우리가 대상함수 혹은 시스템함수를 Full Image로 입력함수을 작은 Patch Image로 매핑하고 Correlation을 구하면, 아래와 같은 결과값을 얻을 수 있습니다.
하단 그림을 보면, 특정 지점에서 진폭값이 최대값을 찍고 있는 것을 확인할 수 있습니다. 이 최대값을 찍고 있는 위치가 Full Image에서 Patch이미지가 위치하고 있는 위치가 됩니다.
 |
 |
|
[ Full Image ] |
[ Patch Image ] |
|
|
|
|
Correlation Result |
|
Convolution
Convolution은 LTI(선형시불변) 시스템에서 입력함수와 시스템 함수 H(x) 이 두가지를 이용하여 출력값을 계산하는 연산을 의미합니다. 이를 통해 나온 출력은 특정 신호가 입력 신호로 주어졌을 때, 특정한 시스템 함수를 갖는 시스템의 출력값은 입력 신호와 시스템 함수의 콘볼루션의 결과가 됩니다.
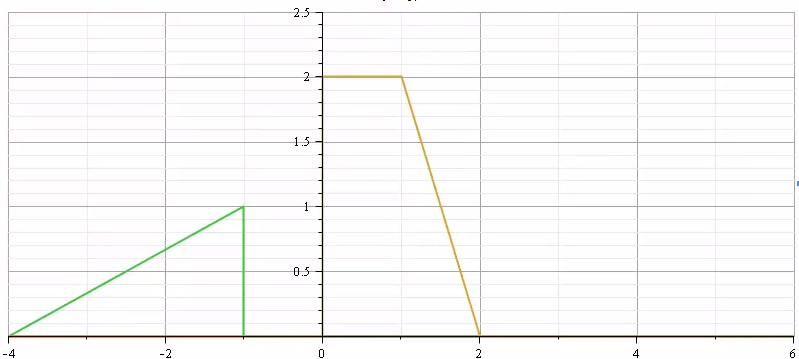
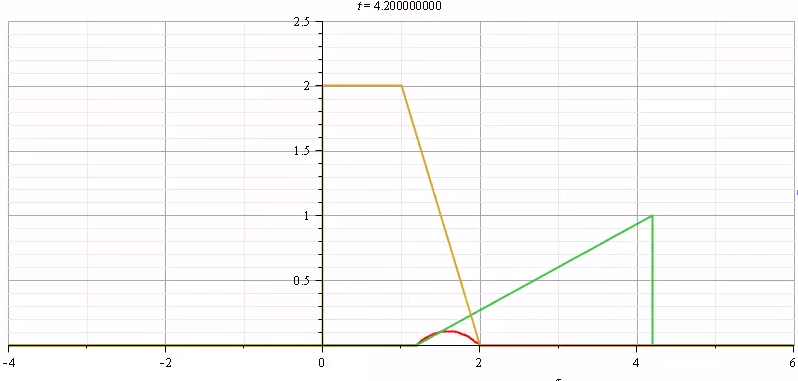
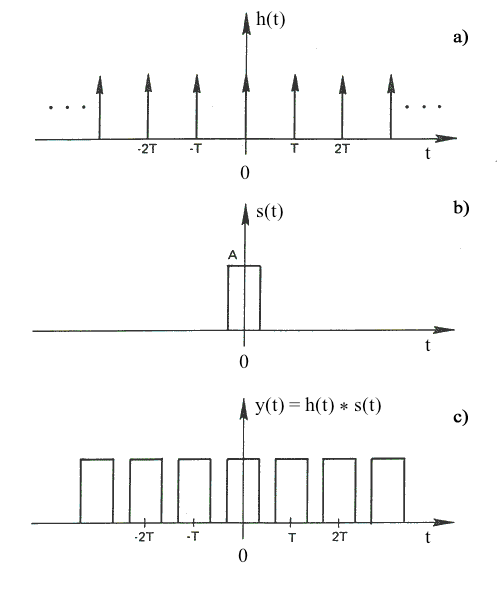
만약 시스템 함수 H(x)가 Rectangle function이고 입력 함수가 Impuse function의 집합일 때, 우리는 아래 그림과 같은 출력값을 얻을 수 있게 됩니다.
하지만 여기서 입력 함수는 대칭 함수이기 때문에, Convolution 연산 시, 좌/우 반전이 되더라도 같은 결과를 갖게 될 것입니다. 하지만 다른 입력 함수가 적용되면 이야기는 달라지게 됩니다.
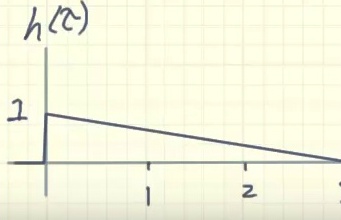
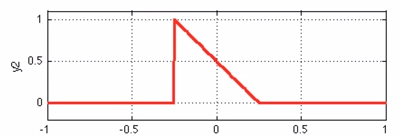
우리가 망치로 어떠한 물체를 길게 누르면서 친다고 가정해봅시다. 입력함수를 f(x)로, 어떠한 물체에 대한 시스템 함수를 H(x)로 하며, 시스템함수는 아래 그림에서의 H(x)와 같이 고정되어있다고 가정합니다. 우리는 우리가 망치로 무언가를 쳤을 때, 해당 충격에 대한 값이 처음에 최대값을 찍고 서서히 떨어지는 모습을 확인하고 이를 통해 입력 함수를 모델링 하였습니다.
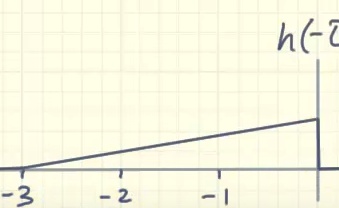
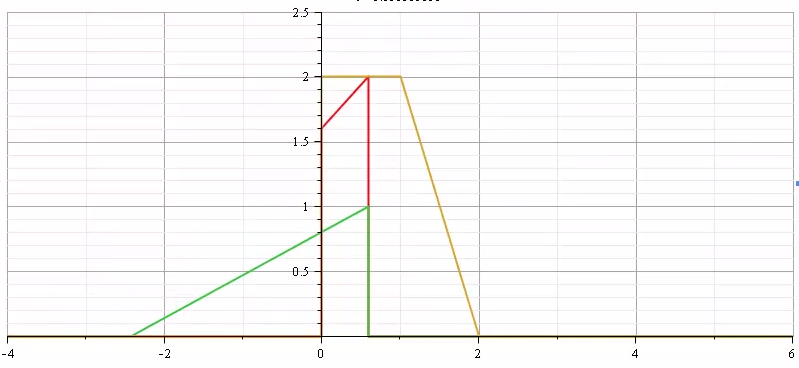
이제 망치를 이용해서 특정 시스템에 충격을 가한다고 상상해 봅시다( 특정 시스템에 입력 함수를 넣음). 이를 시간적인 개념에서 보면, System은 그대로 있고, 망치로 충격을 가하는 것이기 때문에 망치로 길게 누르면서 치는 입력함수는 당연히 좌/우로 반전되서 앞에서부터 미끄러지면서 시스템 함수와 겹치는 넓이를 구해야(sliding window), 특정 입력신호를 특정 시스템에 입력했을 때, 옳은 출력값을 구할 수 있을 것입니다.
이것이 바로 Convolution입니다.
즉, Convolution은 어떤 System function H(x)에 대해서 입력 input function을 주었을 때, 어떠한 output이 나오는가?를 연산해주는 연산자가 됩니다.
|
|
|
|
|
|
|
[ System function H(x) ] |
[ input function f(x) ] |
|
|
|
|
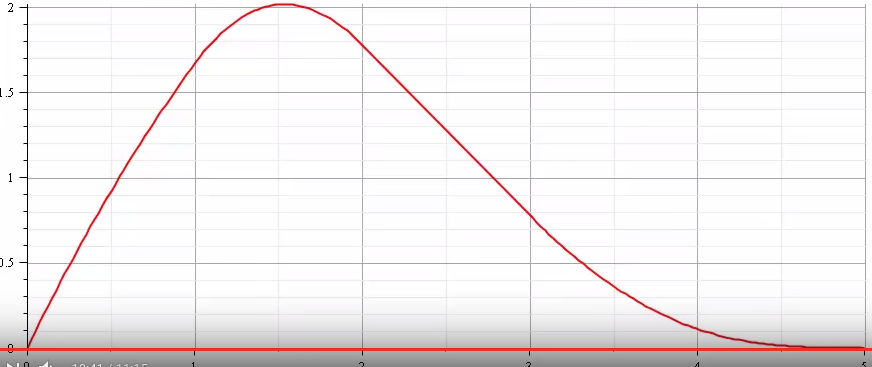
[ Convolution Operation ] |
|
 |
|
|
[ Convolution 결과 ] |
|
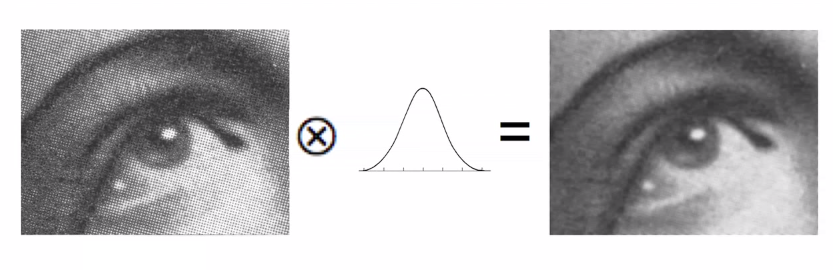
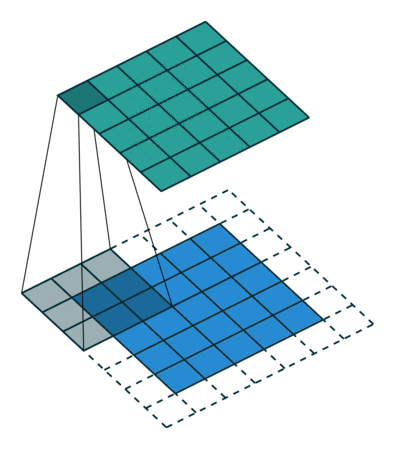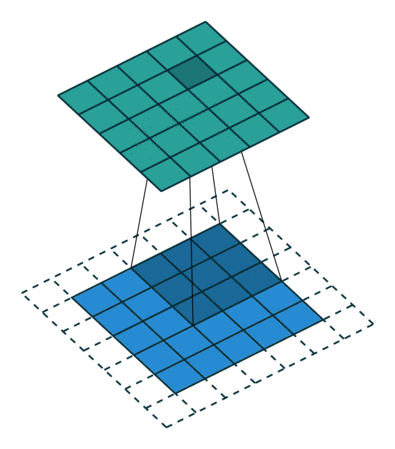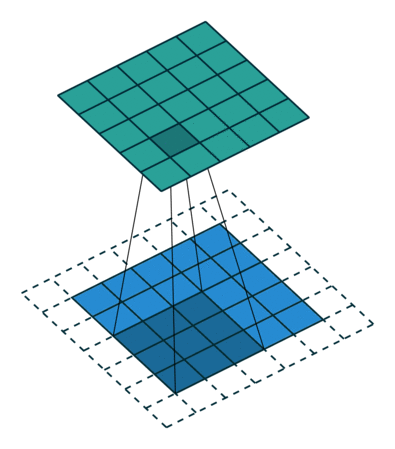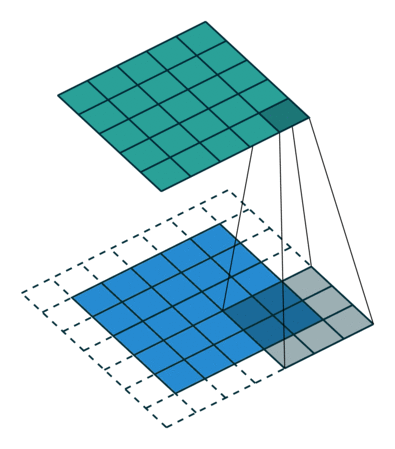
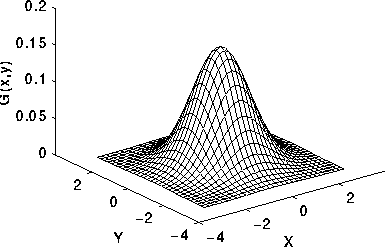
2.영상처리 관점에서의 Convolution
- 아래 그림에서의 가우시안 함수는 1변수 함수.
- image는 2변수 함수.
- 어떻게 convolution을 하면 아래 그림의 오른쪽과 같은 결과가 나오는건가?
이 부분에 대해서 혼자서 곱씹으면서 생각해본 결과 모든 pixel단위에 대해서 가우시안 함수를 convolution하게 되면, 해당 pixel값을 최대값으로 갖고 시스템함수(가우시안)의 분포를 따르는 출력값들을 주변 pixel에 전파(adding) 하게되면서, 같은 결과가 나오지 않을까 않을까라는 생각까지 도달했습니다.
하지만 우리가 영상처리를 공부하다보면 쉽게 접하게 되는 가우시안 blurring에 대한 convolution 연산 방법과 제가 알고있는 Convoltuion 정의에 따른 연산은 너무 상이했습니다.
그래서 더더욱 Convolution을 이해하기가 어려웠습니다. 여태까지 공부하면서 이에 대해서 명확하게 설명해주는 서적이나 자료를 확인하지 못했던 부분도 큰 요인 중 하나지 않을까 싶습니다.
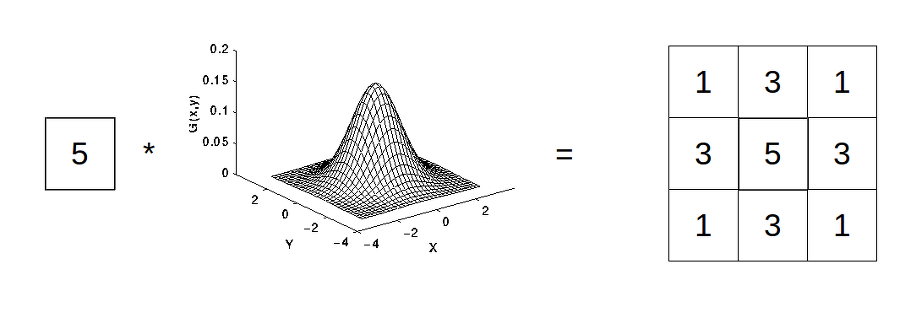
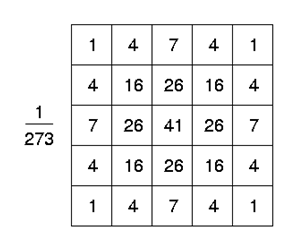
실제 영상처리에서는 가우시안 블러를 Gaussian Kernel Filter를 사용하여 주변 pixel들의 가중치를 고려, 새로운 pixel을 할당하는 방법으로 사용합니다.
분명히 같은 개념이긴 한데, Convolution 혹은 Correlation연산의 정의와는 다르게 사용되고 있음에, 많이 혼란스러웠습니다. 이에 대해서는 아직까지 명확하게 답을 찾지는 못했습니다. 개인적 추측으로는 Convolution정의를 이용한 연산 방법은 매우 복잡하고, 까다롭다는 점과 다른 몇가지 단점 때문에 이에 대한 생각을 살짝 비틀어서 주변 pixel에 대한 가중치를 합해서 새로운 pixel를 만들어내는 방법으로 발전하게되지 않았나 생각해봅니다.
[Reference]
[1]. http://martin.pixelstairs.com/
[2]. http://www.cs.umd.edu/~djacobs/CMSC426/Convolution.pdf
[3]. https://www.youtube.com/watch?v=lsj7XjRbf9o
[4]. https://www.youtube.com/watch?v=O9-HN-yzsFQ
[5]. https://www.youtube.com/watch?v=MQm6ZP1F6ms&t=482s
[6]. https://www.youtube.com/watch?v=C3EEy8adxvc
[7]. https://www.youtube.com/watch?v=zoRJZDiPGds&t=559s
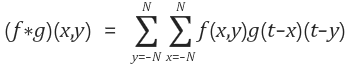
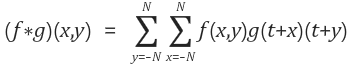

 래
래