Coursera Machine Learning으로 기계학습 배우기 : week2
개요
지난 시간에 이어 Coursera Machine Learning으로 기계학습 배우기 : week2 정리를 진행한다.
목차
해당 포스팅은 연재글로써 지난 연재는 아래의 링크를 참고한다.
글을 읽기에 앞서…
- 본글은 필자가 코세라 기계학습을 공부를 하는 과정에서 개념을 확고히 정리하기 위하는데 목적이 있다. (필자가 나중에 내용을 다시 찾아보기 위한 목적이 있다.)
- 코세라 강의 week 개수에 맞추어 포스팅을 진행할 예정이다.
- 코세라의 슬라이드에 한글 주석을 단것이 핵심으로 내용에서 글을 읽을 필요 없이 슬라이드 그림만으로 최대한 이해가 되게끔 하는데 목적이 있다.
- 수학은 한국의 고등수학을 베이스로 한다. 수학적 개념이 나올때 가급적 고등학교 수학을 베이스로 내용을 정리한다.
- 정리내용의 목차 구성을 코세라 강의와 동일하게 맞추고 또한 제목을 원문으로 둔다. (원본강의 내용과 정리 내용을 서로 서로 찾아보기 쉽게하기 위함이다.)
====================== 2강 ============================================
Multivariate Linear Regression
Multiple Features
Multivariate Linear Regression는 단일 입력변수일때의 선형회귀와 달리 변수가 여러개 들어올때의 선형회귀 개념을 뜻한다. 이를 예제를 통해 배워본다.
아래의 예제는 지난 강의에 계속 설명했던 단일 입력 변수일때의 선형회귀이다.

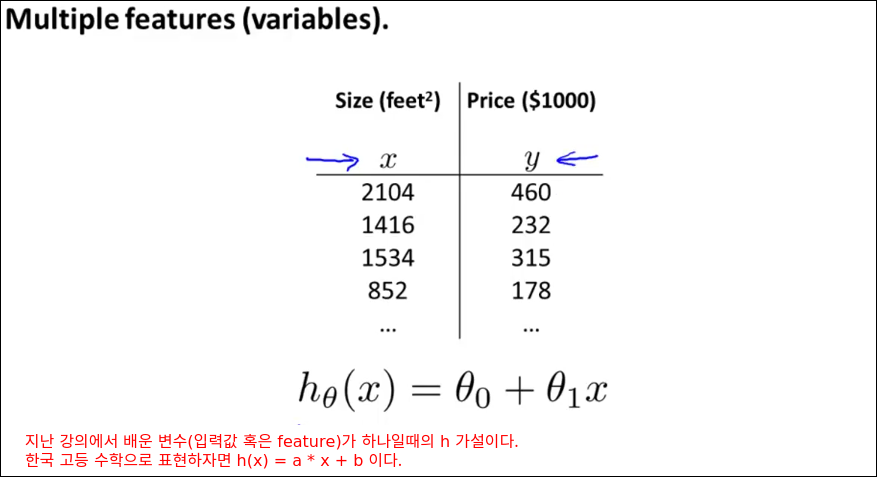
같은 예제가 복합 입력변수가 들어오는 예제로 바뀌었다. 입력변수가 제곱피트 하나에서 제곱피트, 방개수, 층수, 연식 4개로 바뀌었다. 이러한 변화에 대응하기 위해 새로 소개되는 수학기호들을 그림에서 정리한다.

입력 변수가 4개로 바뀌면서 가설 h의 수식도 변화하였다.
만약에 아래 그림의 예제가 학습된 모델이라고 하면 세타값들로 부터 해석이 가능하다. 양수값의 세타는 positive한 영향을 준다는 뜻이고 음수값은 세타는 negative한 영향을 준다는 뜻이다. 예를 들어 연식의 경우 세타값이 -2가 구해졌는데 이 의미는 연식이 될수록 집값에 negative한 영향을 준다는 뜻이다.

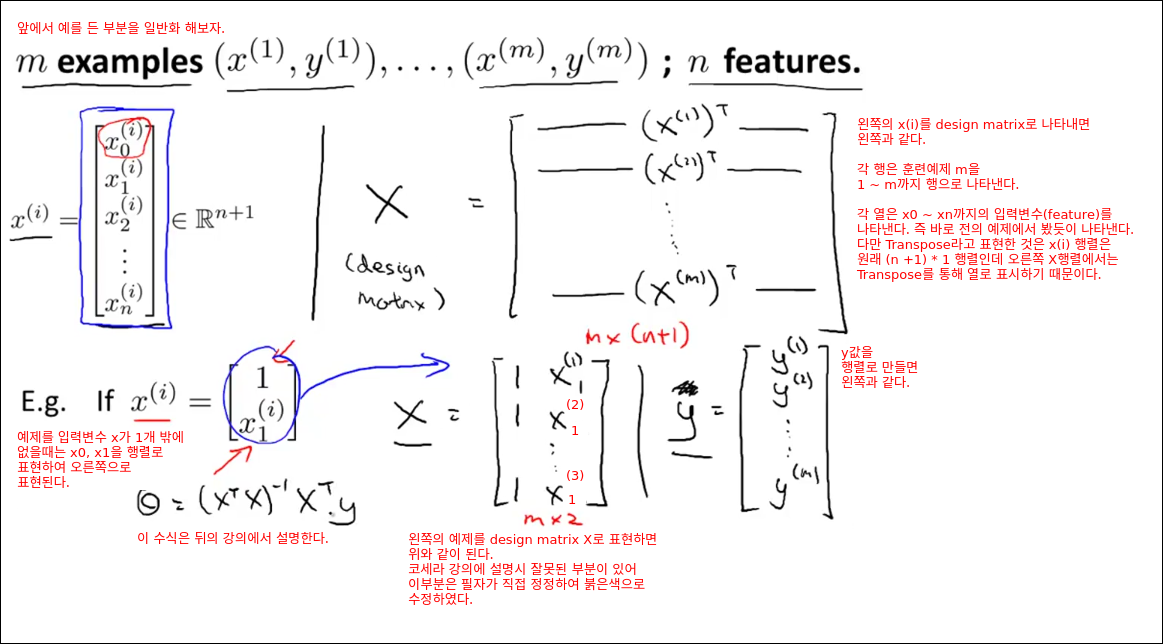
가설 h함수를 수식을 편리하게 바꾸기 위해 x0를 1로 정의하여 세타 0일때도 값을 곱해주면 아래의 h(x) 함수로 바뀐다. 이때 x0, x1 ... xn까지 표현하는 벡터를 X로 정의하고, 세타0, 세타1 ... 세타n가지 표현하는 벡터를 세타로 정의하면 h(x) 함수는 X와 세타의 벡터내적으로 표현할 수 있다. 이는 다시 행렬 연산으로 변환하면 세타의 전체행렬과 x행렬을 곱한것으로 표현 할 수 있다.
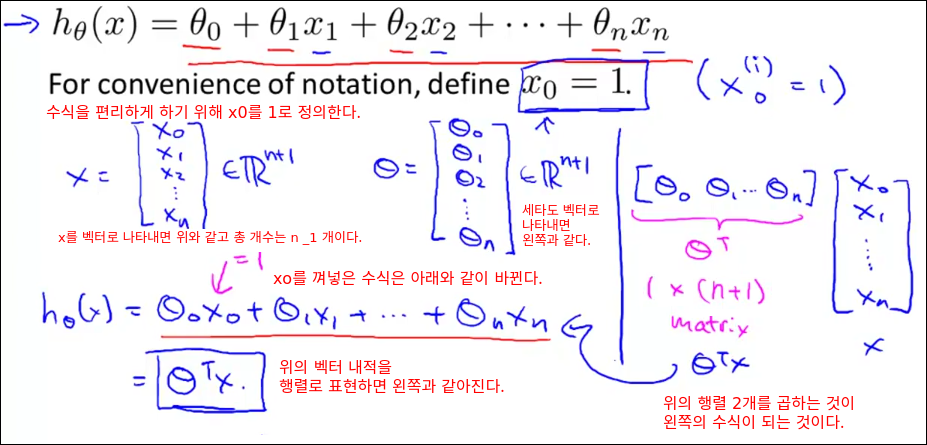
Gradient Descent for Multiple Variables



위의 수식을 최종 정리하자면 아래와 같으 세타0, 세타1, 세타2와 같은 식으로 수식의 규칙성을 가진다.
이부분을 일반화 하면 아래와 같은 세타 j를 반복적으로 구할수 있는 식이 완성된다.

Gradient Descent in Practice I - Feature Scaling
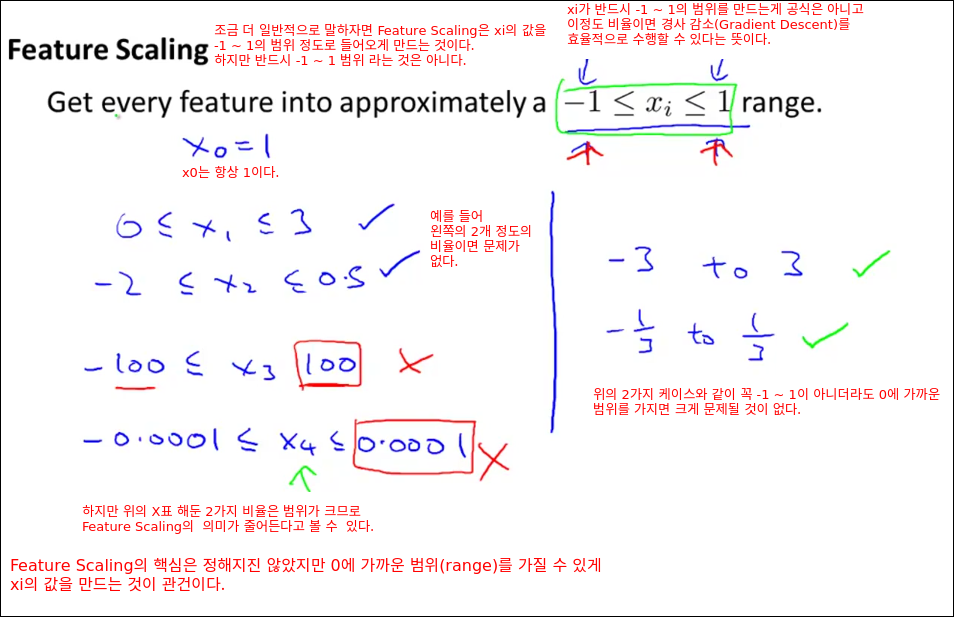
이번 챕터에서는 경사 감소법을 더 효과적으로 활용할 수 있는 트릭을 배운다. 트릭들 중 하나는 Feature Scaling이다. 각 입력값을 정규화 시킨다고 보면 된다.
아이디어는 feature(입력값)들이 비슷한 비율을 가지면 경사감소(Gradient Descent)가 더 빠르게 수렴할 수 있다는 것이다.
파라미터 별로 scale이 다르면 고정된 알파값(학습율)을 설정하는것이 효과적이지 않을수 있다. 따라서 Feature Scaling을 통해 입력변수의 Scale을 동일하게 맞추면 하나의 알파값으로 경사감소의 효과를 볼 수 있다.

 )
)

Mean Normalization은 평균을 0으로 만들어 scale을 줄여주는 방법이다.

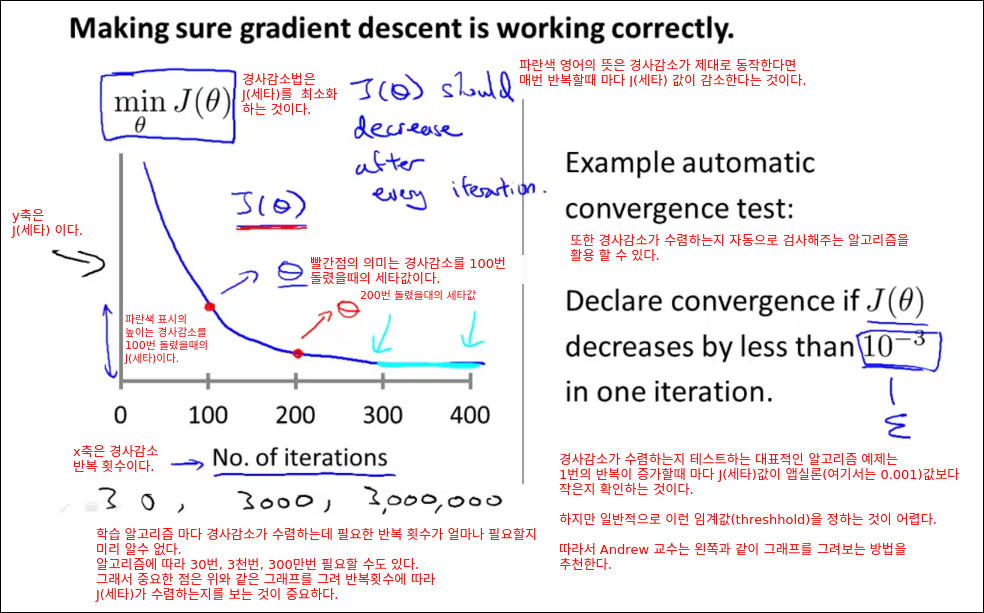
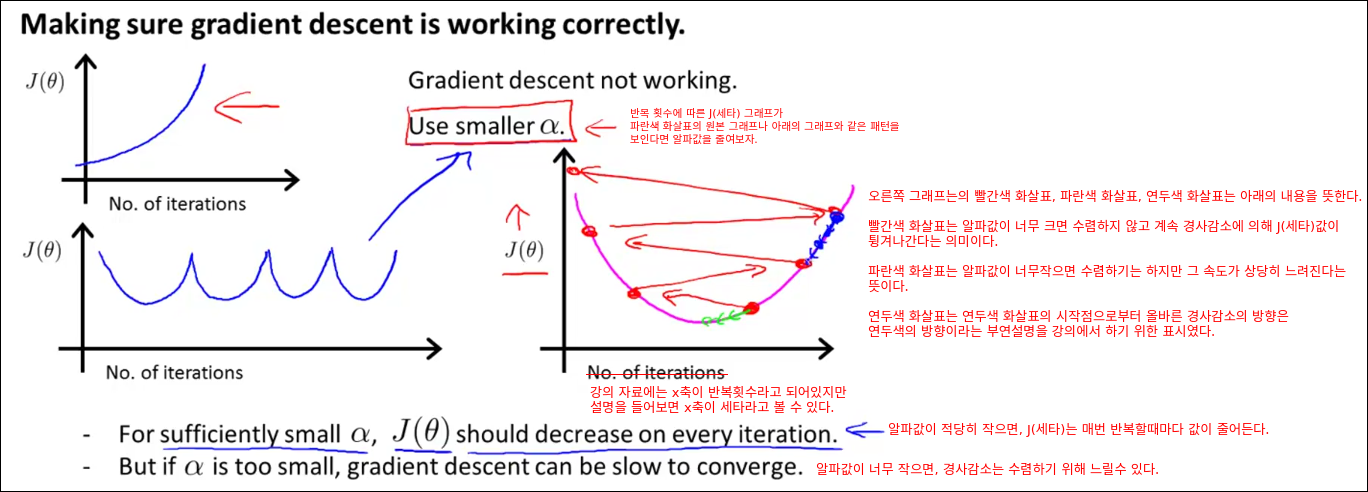
Gradient Descent in Practice II - Learning Rate
이번 챕터에서는 경사 감소법을 더 효과적으로 활용할 수 있는 트릭을 배운다. 이번에 배울 트릭은 Learning Rate 알파에 관한 것이다.



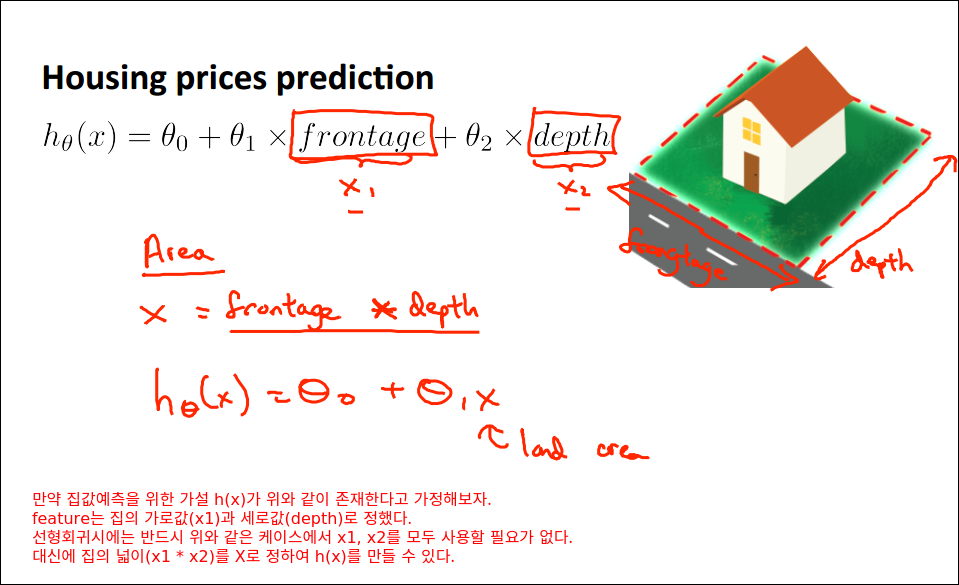
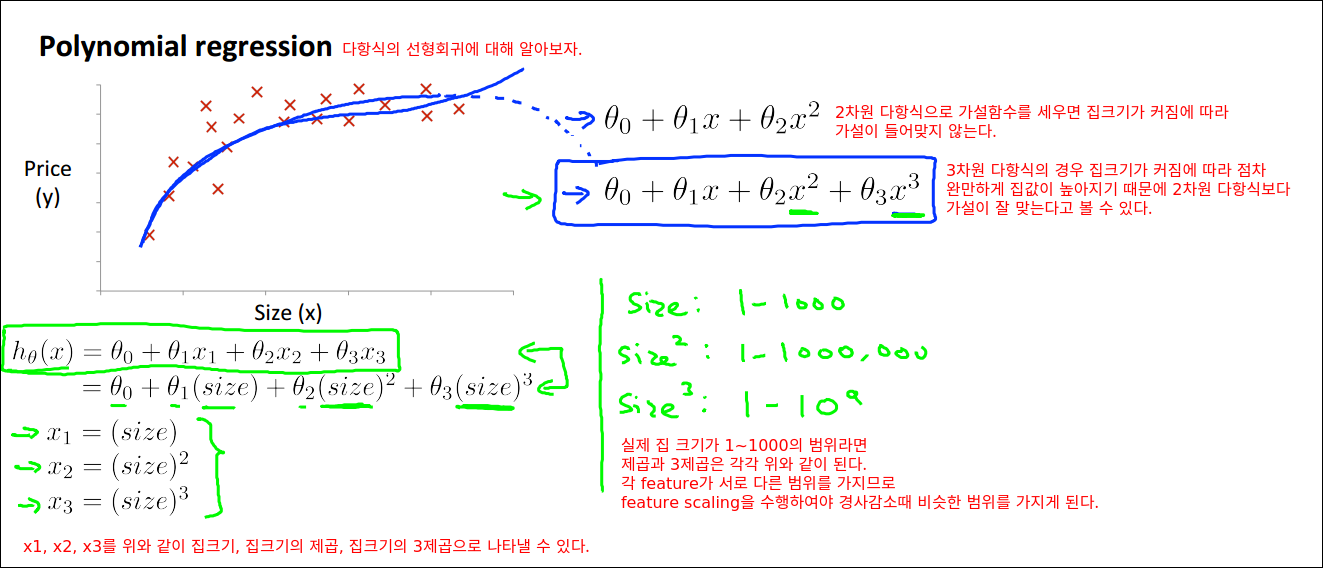
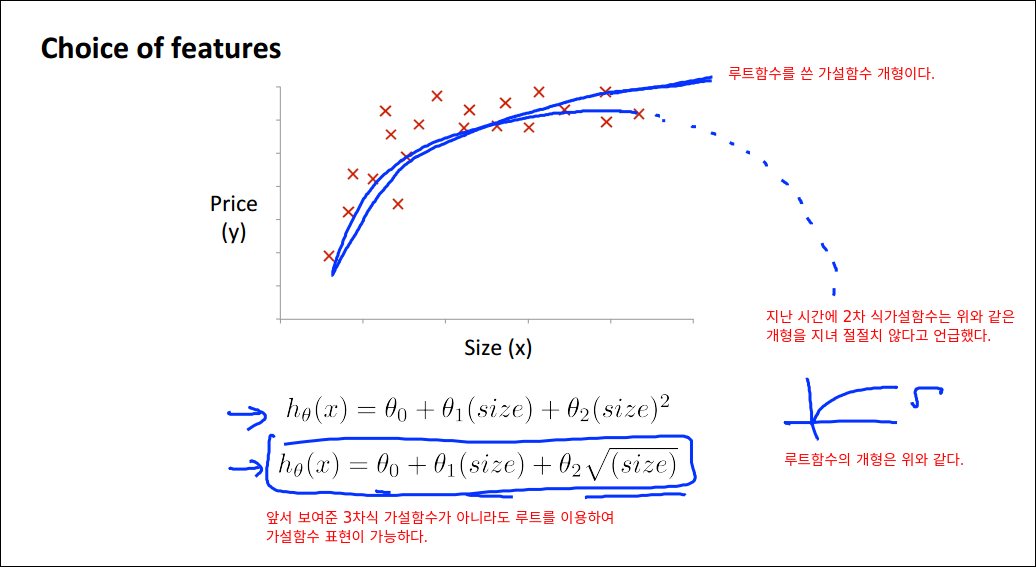
Features and Polynomial Regression

Computing Parameters Analytically
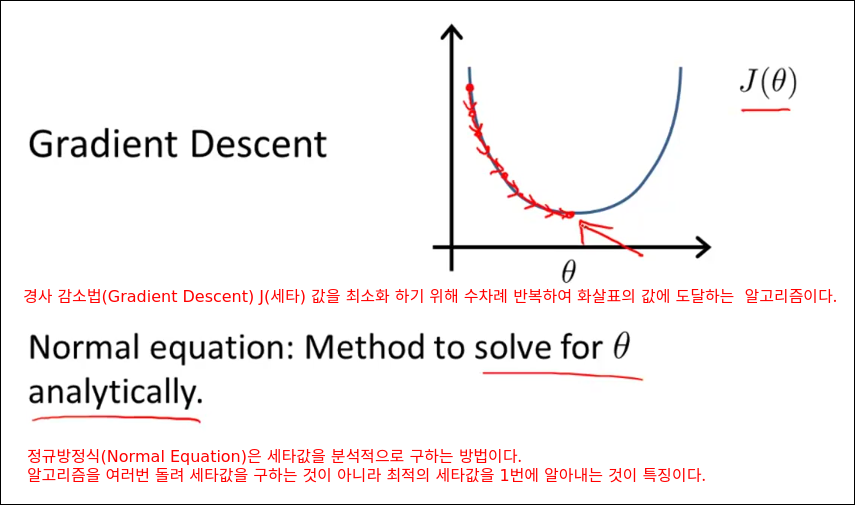
Normal Equation
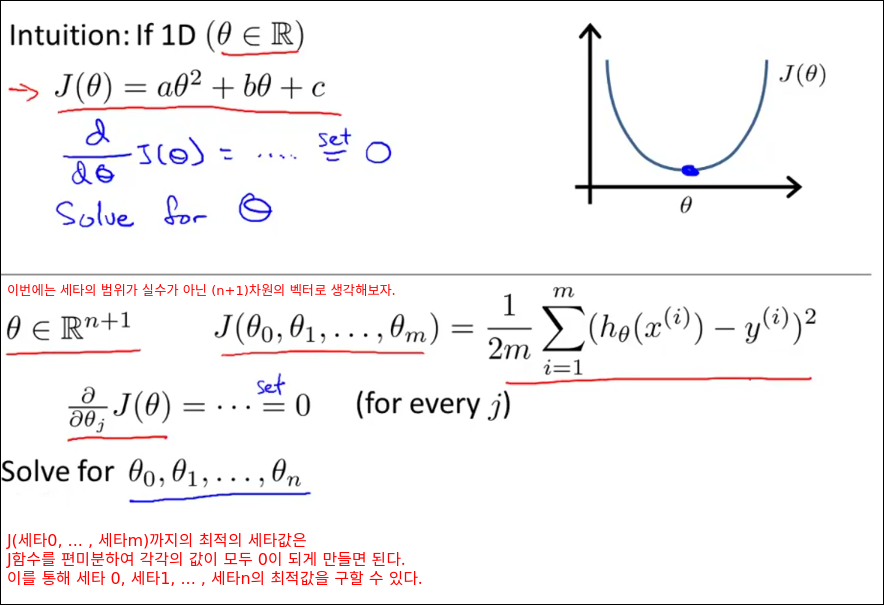
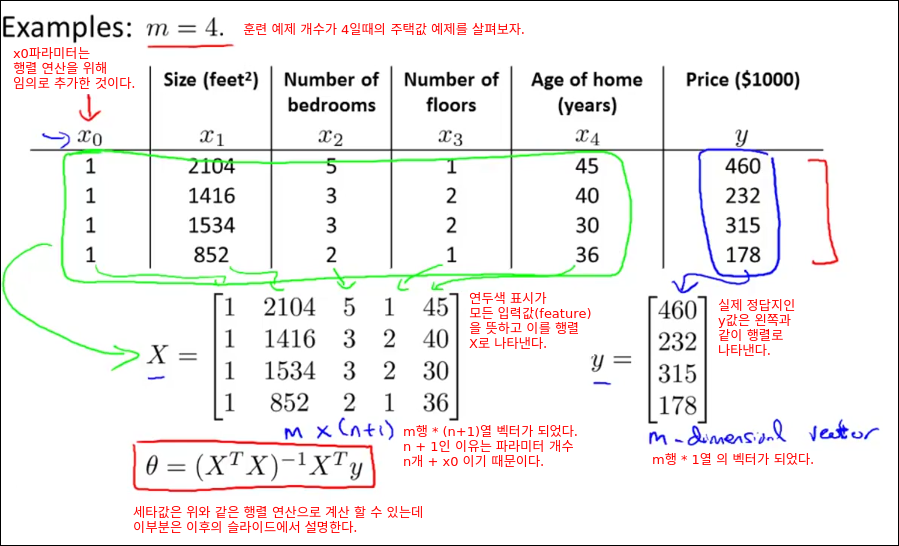
특정 선형 회귀문제에서 세타의 최적 값을 구하는데 효과적인 방법인 Normal Equation을 소개한다.







Normal equation and non-invertibility(optional)
해당 챕터는 앤드류 교수가 선택적으로 더 궁금한 사람만 진행하기를 권장하는 챕터로 SKIP한다.
내용을 들어보면 역행렬이 존재하지 않는 것도 확률적인 것이고 설령 역행렬이 존재하지 않더라도 Octave에서 이를 예외처리 할 수 있는 pinv() 함수가 존재하므로 그리 신경쓰지 않아도 된다고 얘기하고 있다.

Octave/Matlab Tutorial
코세라 강의는 따로 과제실습이 존재하고 이를 수행하기 위해서는 Matlab이나 이와 동일한 오픈소스 Octave로 구현해야 한다. 이 부분을 진행하는데 필요한 기본 Octave 문법을 배워보자.
코세라 강의 내용을 실습하기 위해 Octave, Matlab, Python, NumPy, R등을 사용할 수 있다. 다들 좋은 언어이지만 언어를 익히는데 시간을 너무 쏟지 말고 Octave나 Matlab을 통해 실습을 진행하기를 Andrew 교수가 강력히 추천한다.
필자의 개인적인 의견은 Matlab과 문법이 동일하고 R과도 상당히 흡사하기 때문에 배워두어서 나쁠것은 없다는 것이다.
Basic Operations

옥타브를 실행하면 아래와 같은 화면이 나온다. 필자는 리눅스 환경이고 윈도우즈는 조금 다르게 나올수 있다. 하지만 어차피 프로그램 내에서 프롬프트로 작업을 할 것이기 때문에 차이는 없다.
기본연산
기본 연산은 아래와 같이 가능하다.
1 2 3 4 5 6 7 8 9 10>> 5+6 ans = 11 >> 3-2 ans = 1 >> 5*8 ans = 40 >> 1/2 ans = 0.50000 >> 2^6 ans = 64
논리연산
논리연산은 아래와 같이 수행해 볼 수 있다. 아래 코드에서 유의할 점은 %는 주석 표시로써 연산자가 아니라는 점이다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15<code class="language-text">>> 1 == 2 ans = 0 >> 1 == 2 % false ans = 0 >> 1 != 2 ans = 1 >> 1 && 0 % false ans = 0 >> 1 && 0 % AND ans = 0 >> 1 || 0 % OR ans = 1 >> xor(1,0) ans = 1 </code>
아래 명령어로 파라미터 내 문자열이 프롬프트 출력시 DP되는 문자열을 바꿀 수 있다.
1 2<code class="language-text">PS1('>> ') </code>
변수 할당 및 출력
변수할당 및 출력은 아래와 같다.
1 2 3 4 5 6 7 8 9 10 11<code class="language-text">>> a = 3; >> b = pi; >> a a = 3 >> b ans = 3.1416 >> disp(a); 3 >> disp(sprintf("2 decimals : %0.2f", a)) 2 decimals : 3.00 </code>
벡터
벡터 연산은 아래와 같이 수행한다. 세미콜론은 행을 구분하는 구분자로 한줄에서 입력해도 되고 엔터로 개행을 하면서 입력을 해도 인식한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21<code class="language-text">>> A = [1 2; 3 4; 5 6] A = 1 2 3 4 5 6 >> A = [1 2; 3 4; 5 6] A = 1 2 3 4 5 6 >> V = [1 2 3] V = 1 2 3 >> V = [1; 2; 3] V = 1 2 3 </code>
아래와 같이 지정하면 시작값 1부터 0.1씩 증가하여 2까지 증가하는 벡터를 만든다.
1 2 3 4 5 6 7<code class="language-text">>> v = 1:0.1:2 v = Columns 1 through 7: 1.00000000000000 1.10000000000000 1.20000000000000 1.30000000000000 1.40000000000000 1.50000000000000 1.60000000000000 Columns 8 through 11: 1.70000000000000 1.80000000000000 1.90000000000000 2.00000000000000 </code>
아래와 같은 다양한 방법으로 벡터를 만들 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34<code class="language-text">>> v = 1:6 v = 1 2 3 4 5 6 >> ones(2,3) ans = 1 1 1 1 1 1 >> c = 2 * ones(2,3) c = 2 2 2 2 2 2 >> c = [2 2 2; 2 2 2] c = 2 2 2 2 2 2 >> w = ones(1,3) w = 1 1 1 >> w = zeros(1, 3) w = 0 0 0 >> w = rand(1, 3) w = 0.768905486447251 0.775916317864811 0.497250740474899 >> w = rand(1, 3) w = 0.539191825825911 0.914910175605320 0.813863640693141 >> w = randn(1, 3) w = -0.336876422305242 0.674313193754158 -2.383367379142681 >> w = randn(1, 3) w = -0.301238622307625 2.049211208430472 -1.275134004389243 </code>
아래와 같은 방법으로 수식으로 1만개의 열벡터를 만들고 그래프를 출력할 수 있다.
1 2 3<code class="language-text">>> w = -6 + sqrt(10)*(randn(1, 10000)); >> hist(w) </code>
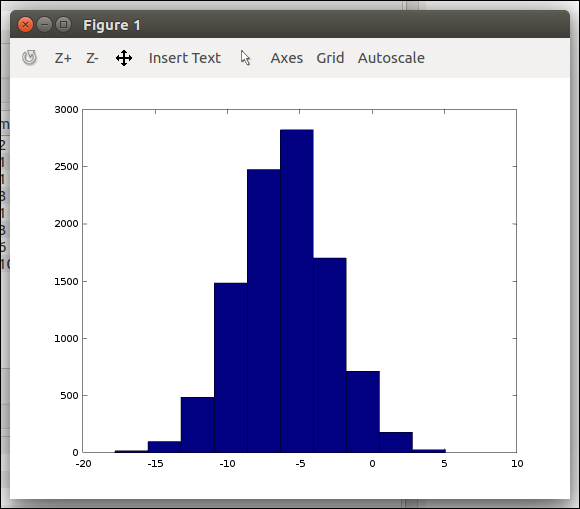
50개의 막대그래프로 보면 아래와 같다.
1 2<code class="language-text">>> hist(w, 50) </code>
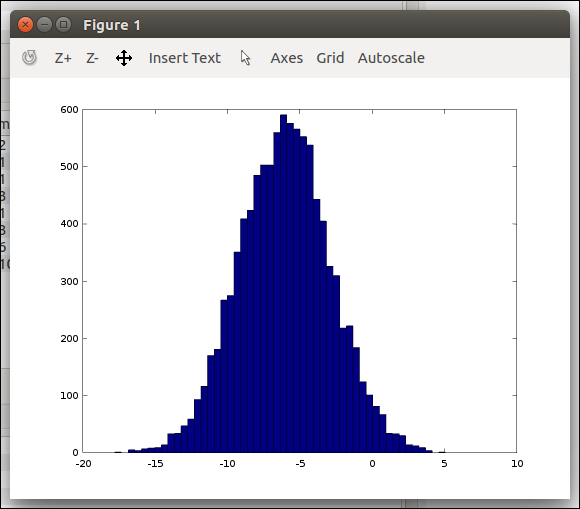
아래와 같은 방법으로 단위행렬 I를 생성할 수 있다.
1 2 3 4 5 6 7 8<code class="language-text">>> I = eye(4) I = Diagonal Matrix 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 </code>
도움말 검색
1 2<code class="language-text">>> help eye </code>
Moving Data Around

행렬 크기 계산
1 2 3 4 5 6 7 8 9 10 11 12 13<code class="language-text">>> A = [1 2; 3 4; 5 6] A = 1 2 3 4 5 6 >> size(A) ans = 3 2 >> size(A, 1) % 행 크기 ans = 3 >> size(A, 2) % 열 크기 ans = 2 </code>
리눅스 명령어 인식
1 2 3<code class="language-text">>> pwd >> ls </code>
feature 읽어오기
1 2<code class="language-text">>> load feature.dat </code>
현재 할당된 변수들 보기
1 2<code class="language-text">>> who </code>
변수 삭제
1 2 3<code class="language-text">>> clear A % 기존에 할당된 A벡터를 지울때 >> clear % 전체 변수 삭제 </code>
벡터 크기 계산
1 2 3 4 5<code class="language-text">>> size(A, 1) ans = 3 >> size(A, 2) ans = 2 </code>
변수 파일로 저장하기
1 2<code class="language-text">>> save test.txt subY; % 파일명이 test.txt, 확장자는 dat나 txt중 취사선택 </code>
행렬 일부 element 지정
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22<code class="language-text">>> A = [1 2; 3 4]; >> >> A(2,1) ans = 3 >> A(2,:) % :은 행 혹은 열 전체를 지칭한다. ans = 3 4 >> A = [1 2; 3 4; 5 6] A = 1 2 3 4 5 6 >> A([1 3], :) % 1행과 3행의 모든 열만 지칭한다. ans = 1 2 5 6 >> A = [ 1 2; 3 4; 5 6] A = 1 2 3 4 5 6 </code>
모든행 특정열에 값 할당
1 2 3 4 5 6<code class="language-text"> >> A(:, 2) = [7 8 9] % 모든행의 2번째 열에 7 8 9를 할당한다. A = 1 7 3 8 5 9 </code>
행렬 Append
1 2 3 4 5 6 7<code class="language-text"> >> A = [A, [100;101;102]]; % 바로 위 상태에서 열을 Append한다. >> A A = 1 7 100 3 8 101 5 9 102 </code>
열벡터로 만들기
1 2 3 4 5 6 7 8 9 10 11 12<code class="language-text">>> A(:) % 위 벡터를 열벡터로 만들어 버린다. ans = 1 3 5 7 8 9 100 101 102 </code>
행렬 이어붙이기
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19<code class="language-text">>> A = [1 2; 3 4] A = 1 2 3 4 >> B = [5 6; 7 8] B = 5 6 7 8 >> C = [A B] % 열로 이어 붙이기 C = 1 2 5 6 3 4 7 8 >> C = [A ; B] % 행으로 이어 붙이기 C = 1 2 3 4 5 6 7 8 </code>
Computing On Data

행렬 곱셈
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31<code class="language-text">>> A = [1 2; 3 4 ; 5 6] A = 1 2 3 4 5 6 >> B = [11 12; 13 14; 15 16] B = 11 12 13 14 15 16 >> C = [1 1; 2 2] C = 1 1 2 2 >> A * C ans = 5 5 11 11 17 17 >> A .*B % 기존의 행렬 곱셈이 아니라 Aij값을 Bij값에 각각 곱함 ans = 11 24 39 56 75 96 >> A .^ 2 % A행렬을 제곱함 ans = 1 4 9 16 25 36 >> V </code>
행렬 나눗셈
1 2 3 4 5 6 7 8 9 10<code class="language-text">V = 1 2 3 >> 1 ./ V % 1/1, 1/2, 1/3으로 계산된다. ans = 1.00000 0.50000 0.33333 </code>
함수 적용
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36<code class="language-text">>> log(V) ans = 0.00000 0.69315 1.09861 >> exp(V) ans = 2.7183 7.3891 20.0855 >> V V = 1 2 3 >> abs(V) ans = 1 2 3 >> max(V) ans = 3 >> V = [1.0 1.5 2.0] V = 1.0000 1.5000 2.0000 >> sum(V) ans = 4.5000 >> prod(V) ans = 3 >> floor(V) ans = 1 1 2 >> ceil(V) ans = 1 2 2 </code>
행렬 변환
1 2 3 4 5 6 7 8 9 10<code class="language-text">>> A A = 1 2 3 4 5 6 >> A' ans = 1 3 5 2 4 6 </code>
Boolean 조건식
1 2 3 4 5 6<code class="language-text">>> V < 3 ans = 1 1 0 </code>
find(V < 3) % 1번째 2번째 인덱스가 V중에서 3보자 작다는 것을 찾아냄 ans =
1 2 3<code class="language-text"> 1 2 </code>
magic 행렬
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20<code class="language-text">>> A = magic(3) A = 8 1 6 3 5 7 4 9 2 >> help magic 'magic' is a function from the file /usr/share/octave/4.0.0/m/special-matrix/magic.m -- Function File: magic (N) Create an N-by-N magic square. A magic square is an arrangement of the integers '1:n^2' such that the row sums, column sums, and diagonal sums are all equal to the same value. Note: N must be greater than 2 for the magic square to exist. Additional help for built-in functions and operators is available in the online version of the manual. Use the command 'doc <topic>' to search the manual index. Help and information about Octave is also available on the WWW at http://www.octave.org and via the help@octave.org mailing list. </code>
단위행렬 I 연산
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22<code class="language-text">>> A A = 8 1 6 3 5 7 4 9 2 >> I = eye(3) I = Diagonal Matrix 1 0 0 0 1 0 0 0 1 >> A * I ans = 8 1 6 3 5 7 4 9 2 >> A .* I ans = 8 0 0 0 5 0 0 0 2 </code>
행렬 회전
1 2 3 4 5 6 7 8 9 10 11 12 13<code class="language-text">>> eye(3) ans = Diagonal Matrix 1 0 0 0 1 0 0 0 1 >> flipud(eye(3)) ans = Permutation Matrix 0 0 1 0 1 0 1 0 0 </code>
역행렬
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16<code class="language-text">>> A = magic(3) A = 8 1 6 3 5 7 4 9 2 >> pinv(A) ans = 0.147222 -0.144444 0.063889 -0.061111 0.022222 0.105556 -0.019444 0.188889 -0.102778 >> A * pinv(A) ans = 1.0000e+00 -1.2157e-14 6.3560e-15 5.5511e-17 1.0000e+00 -1.5266e-16 -5.9813e-15 1.2268e-14 1.0000e+00 </code>
Plotting Data
이 챕터에서는 그래프를 그리는 방법에 대해 문법 및 기능설명을 한다. 따로 어려울것은 없고 필요할 때 찾아서 써보는 것도 방법이다.

sin 함수 그리기
1 2 3 4<code class="language-text">>> t=[0:0.01:0.98]; >> y1 = sin(2*pi*4*t); >> plot(t,y1); </code>
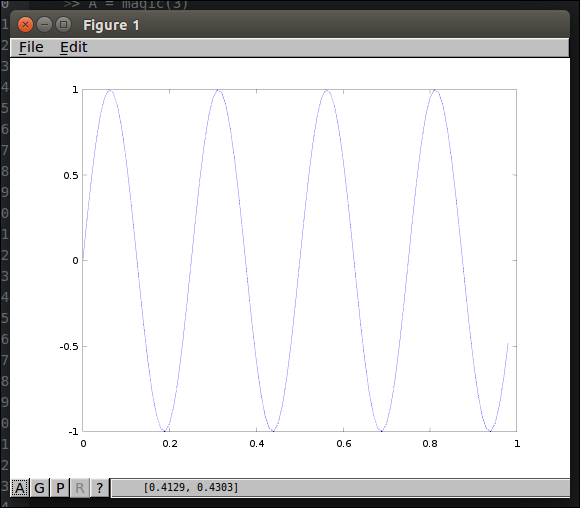
1 2 3<code class="language-text">>> y2=cos(2*pi*4*t); >> plot(t,y2); </code>
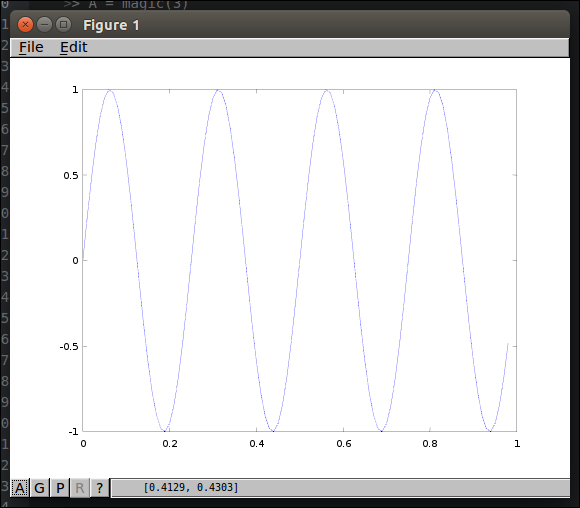
1 2 3 4<code class="language-text">>> plot(t,y1); % 그래프 겹쳐서 2개 그리기 >> hold on >> plot(t,y2, 'r'); % 2번재 그래프는 빨간색 표시 </code>
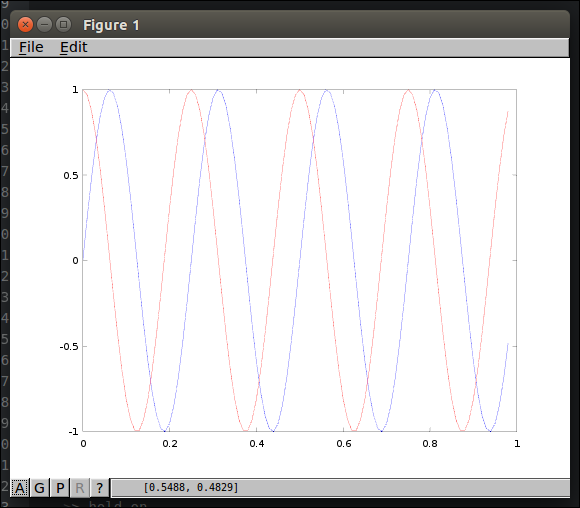
x, y축 레이블 붙이기
1 2 3<code class="language-text">>> xlabel('xlabel'); >> ylabel('ylabel'); </code>
범례 붙이기
1 2<code class="language-text">>> legend('sin', 'cos'); </code>
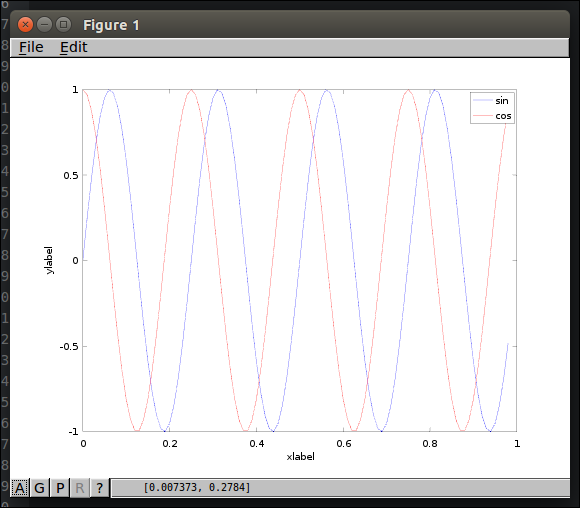
제목 붙이기
1 2<code class="language-text">>> title('title'); </code>
그래프 저장
1 2<code class="language-text">>> print -dpng 'myplot.png'; </code>
그래프 2개의 창으로 띄우기
1 2 3<code class="language-text">>> figure(1);plot(t,y1); >> figure(2);plot(t,y2); </code>
1개의 창에서 그래프 2개 띄우기
1 2 3 4 5 6 7 8<code class="language-text">>> subplot(1,2,1); % 1*2 그리드를 만들어 1번째 그리드에 접근함 >> t=[0:0.01:0.98]; >> y1 = sin(2*pi*4*t); >> plot(t,y1); % 1번째 그리드에 그림 >> subplot(1,2,2); % 1*2 그리드를 만들어 2번째 그리드에 접근함 >> y2=cos(2*pi*4*t); >> plot(t,y2); % 2번째 그리드에 그림 </code>
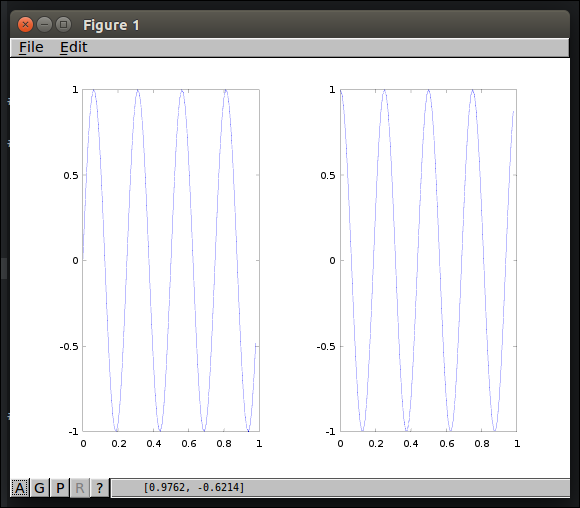
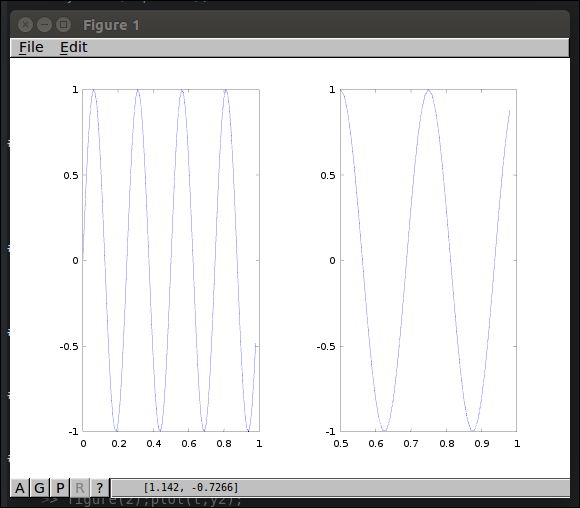
x축 좌표 범위 변경
1 2<code class="language-text">>> axis([0.5 1 -1 1]) % 위의 예제에서 설명하는 것이라 2번째 그리드만 좌표가 바뀜 </code>
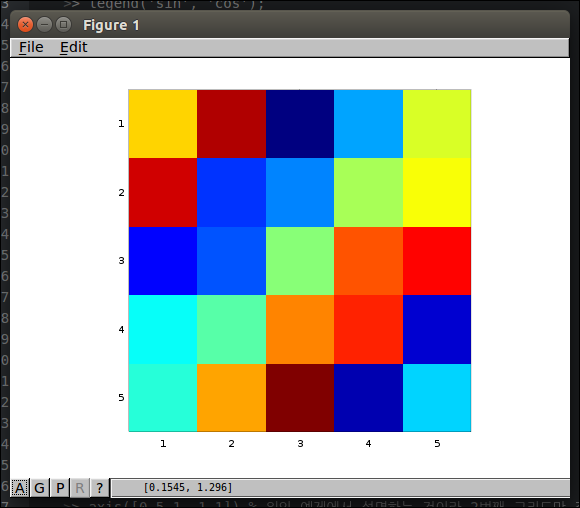
행렬 시각화 하기
1 2 3 4 5 6 7 8 9<code class="language-text">>> A = magic(5) A = 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 >> imagesc(A) </code>
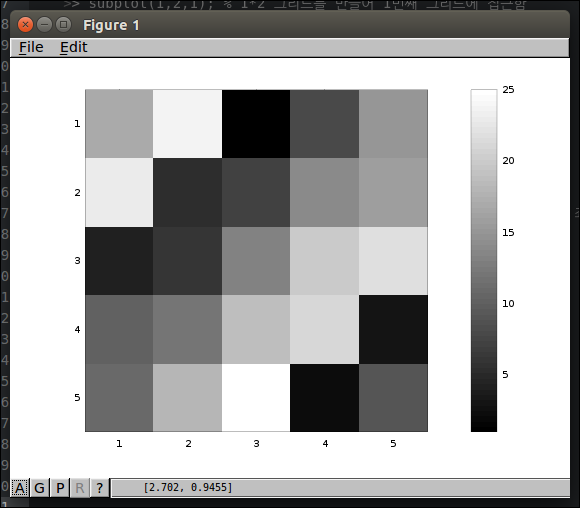
회색 행렬 만들기
행렬의 값에 따라 회색계열의 색깔 농도로 값을 시각화하여 나타낸다.
1 2<code class="language-text">>> imagesc(A), colorbar, colormap gray; </code>
15*15 행렬 시각화
1 2<code class="language-text">>> imagesc(magic(15)) </code>
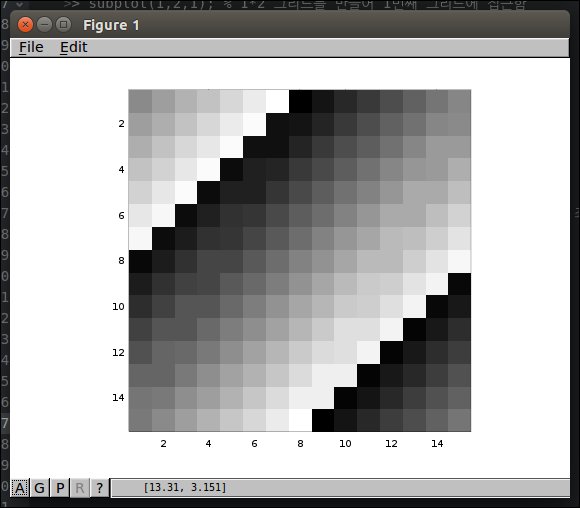
Control Statements; for, while, if, Statements

프로그래밍을 하는 사람 입장에서는 이부분은 어려울것이 전혀 없다.
for 루프
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26<code class="language-text">>> v=zeros(10,1) v = 0 0 0 0 0 0 0 0 0 0 >> for i=1:10, v(i) = 2^i;end; >> v v = 2 4 8 16 32 64 128 256 512 1024 </code>
while 루프
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17<code class="language-text">>> i = 1; while i <= 5, > v(i) = 100; > i = i + 1; > end; >> v v = 100 100 100 100 100 64 128 256 512 1024 </code>
while에 break문 쓰기
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21<code class="language-text">>> i = 1; >> while true, > v(i) = 999; > i = i + 1; > if i == 6, > break; > end; > end; >> v v = 999 999 999 999 999 64 128 256 512 1024 </code>
함수 만들기
Octave가 실행되는 디렉토리에 "hi.m" 이라는 파일명으로 아래 내용 넣기
1 2 3 4 5 6<code class="language-text">function y = hi(x) y = x ^ 2 >> hi(2) % hi.m파일이 있는 경로에서 함수를 실행하면 동작한다. y = 4 ans = 4 </code>
옥타브 탐색경로 추가
아래와 같은 방법으로 현재 디렉토리에 함수가 없더라도 옥타브가 탐색하는 디렉토리 경로를 추가하여 탐색이 일어나게 할 수 있다.
1 2<code class="language-text">>> addpath('경로') </code>
리턴이 2개인 함수
1 2 3 4 5 6 7 8 9<code class="language-text">function [y1, y2] = doubleargs(x) y1 = x^2; y2 = x^3; >> [a, b] = doubleargs(3); >> a a = 9 >> b b = 27 </code>
비용함수 구현해보기
costFunctionJ.m을 아래의 내용으로 만든다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24<code class="language-text">function J = costFunctionJ(X, y, theta) m = size(X,1); % 훈련할 데이터 수 predictions = X * theta; % m개 학습예제의 h(x)들 집합, 논리적으로는 J함수 수식에서 h(x)에 해당한다고 생각하면 됨 sqrErrors = (predictions - y).^2; J = 1 / (2*m) * sum(sqrErrors); >> X = [1 1; 1 2; 1 3] X = 1 1 1 2 1 3 >> Y = [1; 2; 3] Y = 1 2 3 >> theta = [0;1]; >> j = costFunctionJ(X,Y,theta) j = 0 >> theta = [0;0]; >> j = costFunctionJ(X,Y,theta) j = 2.3333 >> (1^2 + 2^2 + 3^2) / (2 * 3) ans = 2.3333 </code>
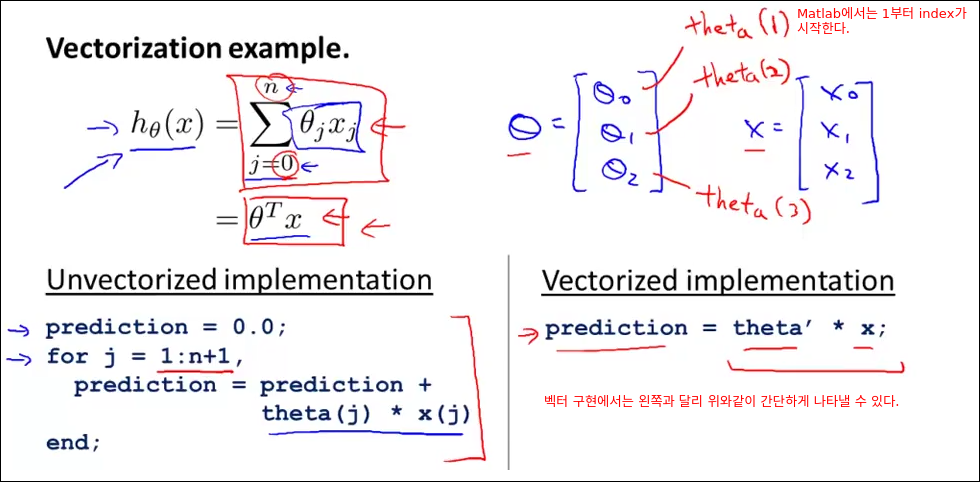
Vectorization
해당 챕터의 핵심은 일반 프로그래밍 언어에서 for 루프로 표현하는 수식이 벡터 계산으로 표현시 어떻게 표현되는지를 알려준다. 또한 벡터 표현이 for loop식 표현에 비해 수식이 간결해져 편리하다는 점을 알려준다.