지난번 <실체가 손에 잡히는 딥러닝> 1편 "인공지능의 세계, 머신러닝과 딥러닝은 어떻게 등장했나"에서는 인공지능과, 머신러닝, 딥러닝의 관계를 짧게 살펴보고, 2편, “인간의 뇌를 모방한 신경망, 그리고 딥러닝”에서는 사람 뇌의 신경세포가 데이터를 처리하는 과정을 이성을 만났을 때 첫인상만으로 호감/비호감을 순식간에 판단하는 사례를 들어 인공적으로 모델링하여 컴퓨터상에서 구현함으로써, 인공 신경망에서 딥러닝이 탄생했는가를 통해 딥러닝의 원리와 구조를 간단히 살펴봤습니다.

이제 딥러닝의 실체를 손에 잡기 위한 마지막 과정으로 넘어가보겠습니다. 앞선 2편 글에서 설명한, 뉴런의 인공신경망 구조는 그림 1과 같습니다.

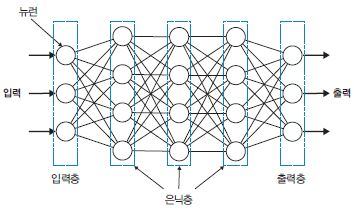
▶ 그림 1 인공 신경망 구조

신경망 구성 요소를 그림으로 이해하기

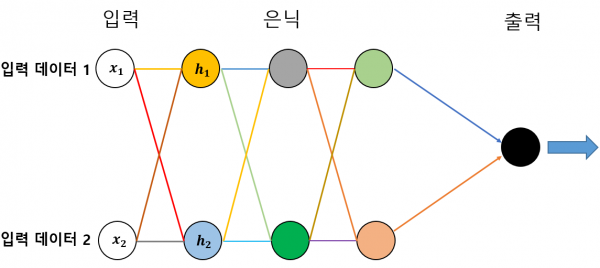
▶ 그림 2 인공 신경망의 데이터 전달 과정

우선, 그림 1을 그림 2처럼 약간 팬시하게 변형해봤습니다. 그림 2에서 원은 하나의 뉴런을 의미하고 뉴런을 연결하는 선은 데이터가 왼쪽에서 오른쪽 방향으로, 뉴런에서 뉴런으로 전달된다는 것을 나타냅니다.

이 인공 신경망으로 데이터 1, 2가 입력된다고 합시다. 이성의 외모로 비친 첫인상으로 호감/비호감을 판단하는 사례라면 이성의 눈 색깔, 코 높이 같은 얼굴 생김생김에 관한 정보들이 입력 데이터입니다. 이 데이터가 오른쪽 방향의 다음 뉴런(h₁, h₂)으로 전달됩니다.

그림을 자세히 보면 알겠지만 입력 데이터 1이 노란색 선으로 전달돼 노란색 뉴런(h₁)으로 표현되었고, 동시에 빨간색 선으로 전달돼 하늘색 뉴런(h₂)으로 표현되었습니다. 또 입력 데이터 2는 황토색 선으로 이어져 노란색 뉴런(h₁)이 되고 회색 선으로 이어져 하늘색 뉴런(h₂)이 됩니다.

이 그림이 의미하는 바가 무엇일까요?

연결선의 색이 다르다는 것은, 예를 들면 입력 데이터 1이 각기 다른 값으로 노란색 뉴런(h₁), 하늘색 뉴런(h₂)에 전달되었다는 의미입니다.

뉴런의 색이 다르다는 것은 노란색 뉴런(h₁)이나 하늘색 뉴런(h₂)이나 모두 같은 입력 데이터1, 2를 전달받았지만 두 개의 데이터를 받아서 처리한 값이 각기 다르다는 의미입니다(물론 같을 수도 있지만 다른 경우가 대부분이라 설명을 위해 색을 다르게 했습니다).

전체 신경망에서 이런 과정을 계속 거친 후 출력층 뉴런에서 최종적인 값(검정색 뉴런)을 만들어 냅니다.

지금 단계에서 우리는 자세한 내부 원리는 몰라도 처음 입력된 데이터들이 계속 다른 값으로 변하면서 뉴런에서 뉴런을 거쳐 출력층으로 나아간다는 것만큼은 분명하게 인지할 수 있다면 전체적인 과정은 이해한 것입니다.

뉴런 하나의 내부 구조

이제 뉴런의 내부를 아주 조금만 더 가까이 들여다 봅시다.

그림 3은 전체 신경망에서 하나의 뉴런을 떼어내 확대해 구성 요소를 나타낸 그림입니다. 입력, 출력, 뉴런은 이미 살펴본 것이지만 가중치, 편향, 활성화 함수라는 용어가 처음으로 등장했네요. 이것들이 무엇인지 하나씩 살펴볼까요. 사실 이것들만 알면 딥러닝을 거의 이해한 것입니다.

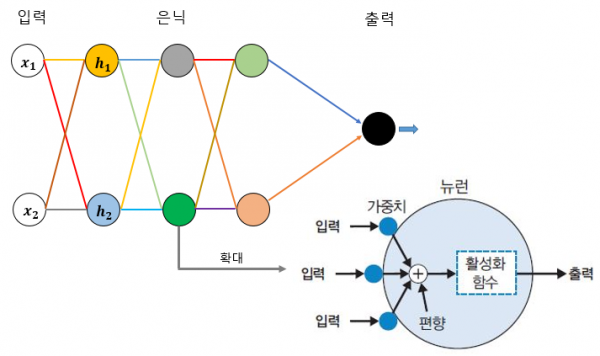
▶ 그림 3 뉴런의 구성 요소

# 가중치란?

뉴런의 연결선 색이 다르다는 것은 입력 데이터 1이 각기 다른 값으로 노란색 뉴런(h₁), 하늘색 뉴런(h₂)으로 전달되었다는 의미라고 앞에서 설명했죠? 데이터 1의 값은 같은데 다른 값으로 전달되려면 이 입력값에 각기 다르게 곱해지는 수치가 있어야겠죠? 이것이 바로 가중치(weight)입니다. 전혀 어려울 것이 없습니다. 가중치라는 원 단어의 뜻을 생각해봐도, 데이터 1을 각기 다른 비중으로 h₁, h₂로 전달시키기 위해 웨이트(weight), 즉 비중(=가중치)을 다르게 한다고 받아들이면 이해하기가 쉬울 겁니다.

# 편향이란?

편향(bias)은 하나의 뉴런으로 입력된 모든 값을 다 더한 다음에(가중합이라고 합니다) 이 값에 더 해주는 상수입니다. 이 값은 하나의 뉴런에서 활성화 함수를 거쳐 최종적으로 출력되는 값을 조절하는 역할을 합니다. 순서상 편향이 먼저 나왔지만 다음에 설명할 활성화 함수를 알게 되면 이 값의 역할도 쉽게 이해됩니다.

# 활성화 함수란?

우리가 사는 세상을 한번 생각해 봅시다. 실제 세계에서는 입력값에 비례해서 출력값이 나오지가 않을 때도 많습니다. 대개는 어떤 임계점이 있고 그 임계점을 경계로 큰 변화가 생깁니다. 물이 끓는 것도 그렇고 비행기가 이륙하는 것도 그렇습니다.

마찬가지로 뇌의 뉴런도 하나의 뉴런에서 다른 뉴런으로 신호를 전달할 때 어떤 임계점을 경계로 출력값에 큰 변화가 있는 것으로 추정됩니다.

인공 신경망은 디지털 세계이긴 하지만 뇌의 구조를 모방하므로 임계점을 설정하고 출력값에 변화를 주는 함수를 이용합니다. 이 활성화 함수 덕분에 2편에서 설명한 은닉층으로 인한 좌표평면 왜곡효과도 발생합니다. 앞에서 설명한 편향은 임계점을 얼마나 쉽게 넘을지 말지를 조절해주는 값이라고 생각하면 됩니다.

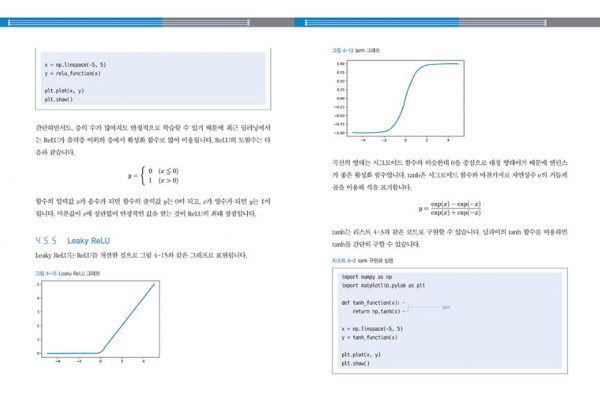
활성화 함수에는 시그모이드(Sigmoid) 함수, 렐루(ReLU) 함수, 항등 함수, 소프트맥스 등 여러 종류가 있는데 이처럼 다양한 활성화 함수는 <실체가 손에 잡히는 딥러닝, 기초부터 실전 프로그래밍> 4.5절에 코드와 함께 결과를 보여주면서 설명하고 있으니 참고하시기 바랍니다. (아래 책 내용을 크게 해서 보세요)

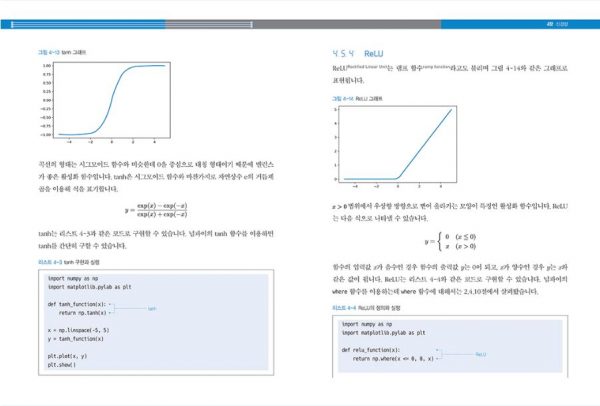
이제 한번 종합해 봅시다. 층이 많은 인공 신경망은(딥러닝)은 데이터를 입력받아 그 데이터들에 각기 다른 가중치를 곱해 다음 층의 뉴런으로 전달하는 과정을 반복적으로 거치면서 마지막에 최종적인 출력값을 계산합니다. 그렇다면 이 과정에서 구체적으로 계산해야 되는 수치들은 무엇일까요? 그림 4를 한번 봅시다.

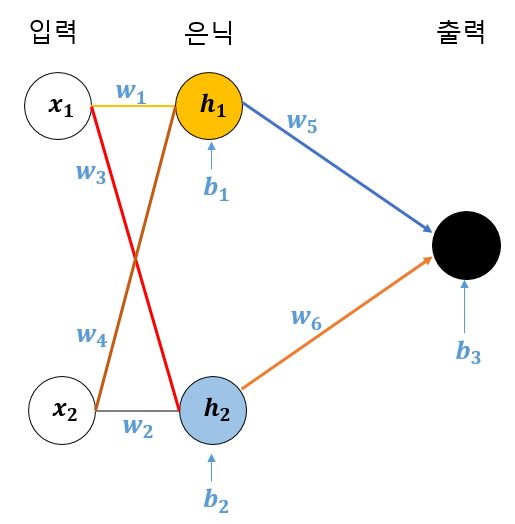
▶ 그림 4 인공 신경망에서 계산해야 되는 값들

이 신경망에서 원(뉴런) 안에 있는 값은 이미 알고 있거나(입력 데이터1, 2), 가중치와 편향, 활성화 함수만 알면 구할 수 있는 값들입니다.

문제는 파란색으로 나타낸 가중치(w₁, w₂, …..)와 편향(b₁, b₂,…..) 값입니다. 이 값들은 기존 데이터를 학습해서 가장 적절한 값들을 찾아내야 하는 수치로서, 성능이 좋은 딥러닝을 구축한다는 것은 결국 이 수치들의 최적값을 구해야 하는 것입니다.

그럼 가중치와 편향을 구하는 원리와 과정은 어떻게 이뤄지는지 알아봅시다.

역전파를 통해 최적의 가중치와 편향 구하기

드디어 역전파라는 단어가 등장했네요. 일단 잠시 잊어두셔도 좋으시니 신경을 꺼두세요.

처음에는 최적의 가중치와 편향을 모르니까 일단은 임의로 설정합니다. 다음 그림 5를 보면, 입력 데이터를 받아 임의로 설정된 가중치를 곱하고 편향을 더해 뉴런에서 뉴런으로 전달한 뒤 최종적으로 출력값 1을 얻었고, 그런데 실젯값(정답)이 7이라고 가정합시다. 그럼 6만큼의 차이(오류)가 생겼네요.

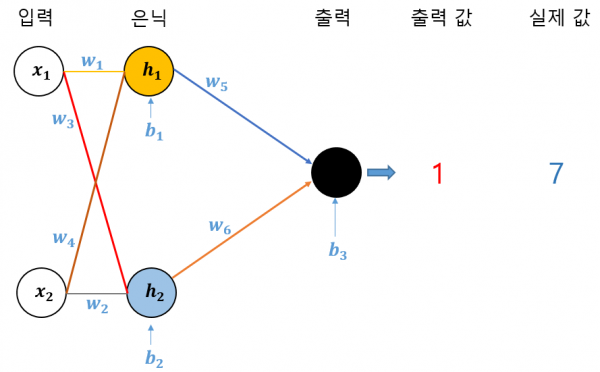
▶ 그림 5 임의 설정된 가중치와 편향으로 출력된 값과 실젯값 차이

이 결과를 보면 처음에 임의로 설정한 가중치들과 편향은 적절한 값이 아니라는 것이 분명해졌습니다. 그렇다면 이제 가중치와 편향을 다른 값으로 바꿔야죠.

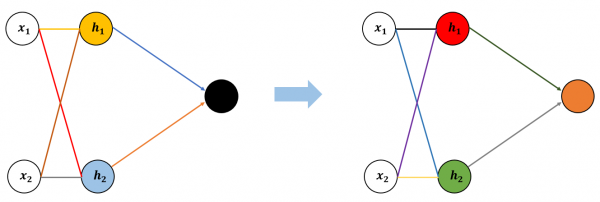
▶ 그림 6 새로운 가중치와 편향 설정

그림 6처럼 아예 다른 가중치와 편향을 임의로 설정하는 방법이 있지만, 뉴런의 수가 많은 경우에는 가중치와 편향의 가능한 조합이 무한대라 사실상 이 방법은 불가능합니다. 그래서 사용하는 방법은 그림 7처럼 처음 설정한 신경망 구조를 조금씩, 계속 개선하는 방법입니다. 여기서는 색으로 구분해서 표현해보겠습니다.

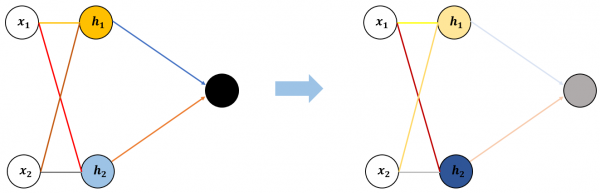
▶ 그림 7 가중치와 편향을 조금씩 개선

그림 6과의 차이점이 보이나요? 초기에 설정한 신경망 구조를 아주 조금만 변화시켰습니다. 오른편의 바뀐 신경망에서 연결선과 뉴런의 색이 처음(왼쪽)보다 아주 조금 바뀌었죠. 구조를 조금 바꾼다는 것은 각 가중치와 편향 값을 처음 설정한 값에서 아주 조금만 변화시킨다는 의미입니다.

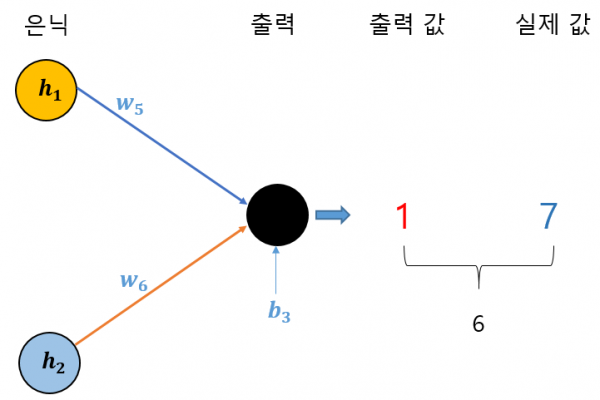
▶ 그림 8 가중치와 편향 수정

그림 8은 최종 은닉층과 출력층만 떼어낸 그림입니다. 이제 출력값과 실젯값의 차이는 6입니다. 이 차이 6을 만들어내는데 w₅, w₆, b₃이 일정부분 역할을 했겠죠? 그래서 차이(오류)를 줄이는 방향으로 w₅, w₆, b₃도 조금 바꾸자는 것입니다.

그림에서는 그냥 차이(오류)가 6이다고 설명했지만, 실제로는 (출력값 – 실젯값)² 의 수식으로 표현합니다(이를 손실 함수라고 합니다). 이 식은 당연히 값을 만드는 데 기여하는 w₅, w₆, b₃을 포함합니다.

이때 아주 작은 w₅의 변화량에 따른 (출력값 – 실젯값)²의 변화량을 구할 수 있습니다. 이를 다른 말로 표현하면 (출력값 – 차이값)²를 w₅로 미분한다고 하죠. 처음 설정한 w₅ 값은 차이(오류)를 줄이는 방향으로 다음과 같이 조금 수정할 수 있습니다.

새로운 w₅ = 기존 w₅ – η* { (출력값 – 실젯값)² }을 w₅로 미분한 값

새로운 w₅를 구한 것처럼 신경망을 구성하는 모든 가중치와 편향을 위의 방식(출력값과 실젯값의 차이를 조금 줄이는 방식)으로 오른쪽(출력층)에서 왼쪽(입력층) 방향으로 역방향으로 하나씩 수정합니다. 그림 9는 이 과정을 표현한 것입니다.

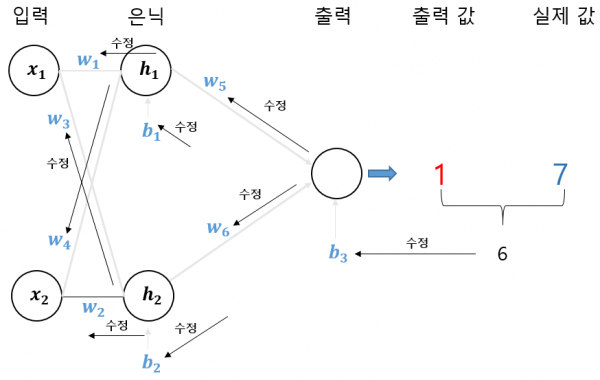
▶ 그림 9 역전파에 의한 가중치와 편향 수정

이런 방식으로 새로운 가중치와 편향을 구하면 그림 7처럼 처음 설정한 신경망 구조를 아주 조금 개선한 새로운 신경망을 구축할 수 있습니다.

그럼 이 다음에는 어떻게 하는건가요?

조금 개선한 신경망으로 새로운 출력값을 구하고 다시 실젯값과의 차이를 구한 다음 이 차이를 또 줄이도록 모든 가중치와 편향을 조금 수정합니다. 이 과정을 계속 반복하다보면 어느 시점에이르러 최적화된 가중치와 편향 값을 구할 수 있겠죠? 이것이 바로 역전파(backpropagation), 즉 오차의 역전파라고 부르는 방법이며 딥러닝의 실체이자 핵심입니다. 역전파에 대해서는 <실체가 손에 잡히는 딥러닝, 기초부터 실전 프로그래밍> 책에 좀 더 자세하게 설명되어 있으니 참고하시기 바랍니다.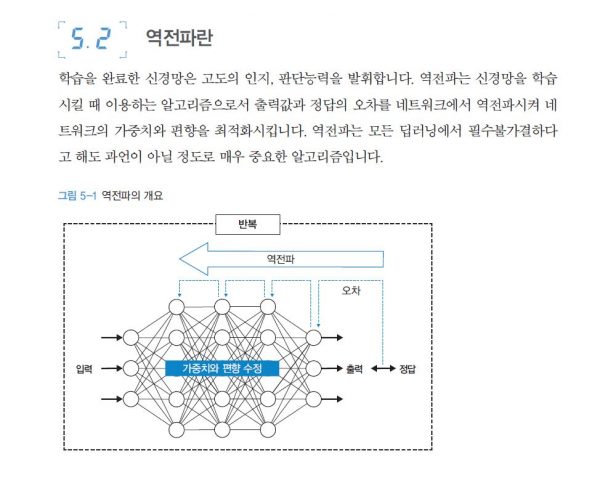

<실체가 손에 잡히는 딥러닝> 연재를 마치며

사실 딥러닝을 단 3회에 걸쳐 이렇게 간단하게 설명해도 될지 약간 걱정스럽기도 하지만 핵심적인 내용을 이해하는 것이 더 높은 단계에 더 빨리 쉽게, 도달할 수 있는 지름길이라는 믿음으로 제 나름의 방법으로 딥러닝의 실체와 원리를 설명해보았습니다. 쉽게 설명하느라 미처 다루지 못한 많은 내용들은 제가 번역한 <실체가 손에 잡히는 딥러닝, 기초부터 실전 프로그래밍>을 참고하시면 많은 도움이 될 것이라고 믿습니다.

실제 업무에서 딥러닝을 사용하기 위해서는 더 알아야 할 것들이 훨씬 많지만 모든 것이 그렇듯 첫 시작이 중요하다고 생각합니다. 이 연재글을 읽고 딥러닝에 대해 조금이라도 호기심이 생긴 분들이 있다면 글을 쓴 보람이 있을 것 같습니다. 다음에는 또 다른 주제로 찾아 뵙겠습니다. 부족한 글을 읽어 주신 많은 분들에게 감사의 말씀 드립니다.